数据结构与算法

摆烂了挺久，零零散散的终于完成数据结构与算法的部分内容学习，不过感觉这玩意仿佛就学习的那一段时间记得比较

清楚，过段时间就忘了干净了，还是比较难消化的。抛开学习上的事情以外，因为这疫情的持续影响最近感觉挺多事情

都不太顺利，无论是求职还是生活的各方面，自己正如11、12月寒冬中熄灭的火种一般，也许这就是所谓的时代的一粒

沙,落在每个人肩头都是一座大山，唉。

数据结构

1.线性结构

特点：数据元素之间存在一对一的线性关系

有两种存储结构：

• 顺序存储结构
  • 顺序存储的线性表称为顺序表，其中存储的元素的内存空间都是连续的
• 链式存储结构
  • 链式存储的线性表称为链表，其中的存储元素的内存空间不一定是连续的，元素节点中存放数据元素以及相邻元素的地址信息

线性结构常见的有：数组、队列、链表和栈

2.非线性结构

非线性结构有：二维数组、多维数组、广义表、树结构、图结构

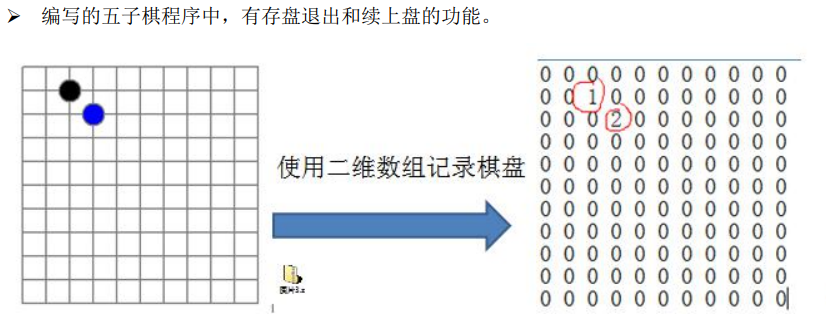
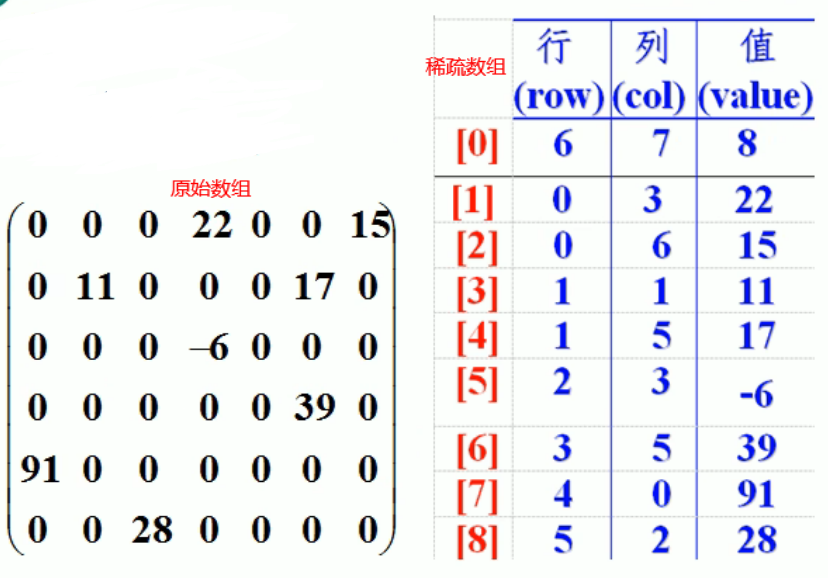
稀疏数组

定义：当一个数组内的大部分元素都为0，或都是同一个值时，可以考虑使用稀疏数组保存这个数组

处理方法：①记录数组总共几行几列，有多少个不同的值

​ ②把不同值元素的行列值记录在一个小型数组中，从而缩小程序的规模

思路分析：二维数组 —> 稀疏数组 —> 转换为文件 (且可以逆转)

public class SparseArray {
    /**
     * Description : 将二维数组转换为稀疏数组
     **/
    public static void main(String[] args) {
        //原始数组
        int[][] array = new int[11][11];
        array[1][2] = 1;
        array[2][3] = 2;
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                System.out.print(array[i][j] + "\t");
            }
            System.out.println();
        }

        //统计数组中元素不为0的元素
        int sum = 0;
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                if(array[i][j] != 0){
                    sum += 1;
                }
            }
        }
        System.out.println("========================");
        //创建稀疏数组
        int[][] sparseArray = new int[sum+1][3];
        sparseArray[0][0] = 11;
        sparseArray[0][1] = 11;
        sparseArray[0][2] = sum;

        //将二维数组中的非0元素放到稀疏数组中
        int count = 0;//用于记录是第几个非0的元素
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array[i].length; j++) {
                if(array[i][j] != 0 ){
                        count++;
                        sparseArray[count][0] = i;
                        sparseArray[count][1] = j;
                        sparseArray[count][2] = array[i][j];
                }
            }
        }

        //遍历稀疏数组
        for (int i = 0; i < sparseArray.length; i++) {
            for (int j = 0; j < sparseArray[i].length; j++) {
                System.out.print(sparseArray[i][j] + "\t");
            }
            System.out.println();
        }

        System.out.println("========================");
        /**
         * Description : 将稀疏数组恢复为二维数组
         */
         //创建一个新的二维数组

        int[][] theNewArray = new int[sparseArray[0][0]][sparseArray[0][1]];
        //方式一
        for (int i = 1; i < sparseArray.length; i++) {
             theNewArray[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];
        }

        //输出新的二维数组
        for (int i = 0; i < theNewArray.length; i++) {
            for (int j = 0; j < theNewArray[i].length; j++) {
                System.out.print(theNewArray[i][j] + "\t");
            }
            System.out.println();
        }
    }
}

队列

• 队列是一个有序列表，可以用数组或链表来实现

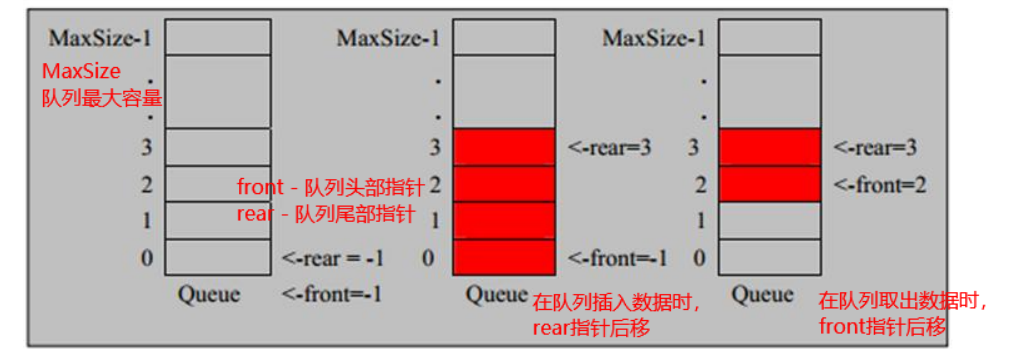
特点：先进先出原则(即先存入的数据要先取出，后存入的数据后取出)，队列的左端为队头,右端为队尾

public class QueueArray1 {
    private int front; 
    //队列头部指针
    private int rear; //队列尾部指针
    private int[] queueArray; //队列数组，用于存放数据
    private int maxSize; //表示数组的最大容量
 
    public QueueArray1() {
    }

     //创建队列的构造器
    public QueueArray1(int maxSize) {
        this.front = -1;//队列头部指针,指向队列头的前一个位置
        this.rear = -1;//队列尾部指针，指向队列尾的具体的数据
        this.queueArray = new int[maxSize];
        this.maxSize = maxSize;
    }

    //判断队列是否未满
    public boolean queueIsFull(){
        return rear == maxSize-1;
    }

    //判断队列是否为空
    public boolean queueIsEmpty(){
        return front == rear;
    }

    //添加数据到队列中
    public void addDataInQueue(int num){
        //判断队列是否已满
        if (queueIsFull()){
            throw new RuntimeException("队列已满,无法添加数据");
        }else{
            rear++;
            queueArray[rear] = num;
        }
    }

    //从队列中获取数据
    public int getDataFromQueue(){
        //判断队列数组是否为空
        if (queueIsEmpty()){
            //由于数组中有可能存在-1的值，故采取抛出一个异常进行提示
            throw new RuntimeException("队列没有任何数据，获取失败");
        }
        front++; //front后移
        return queueArray[front];
    }

    //显示队列的所有数据
    public void showQueue(){
        if (queueIsEmpty()){
            throw new RuntimeException("队列没有任何数据");
        }else {
            for (int i = 0; i < queueArray.length; i++) {
                System.out.print(queueArray[i] + "\t");
                if (i == queueArray.length - 1){
                    System.out.println();
                }
            }
        }
    }

    //显示队列的头数据(不是取出数据)
    public int showTheFirst(){
        if (queueIsEmpty()){
            throw new RuntimeException("队列为空");
        }else{
            return queueArray[front+1];
        }
    }

}

直接使用数组模拟队列存在一个问题：即当队列的所有数据取出后依然无法往队列中添加数据

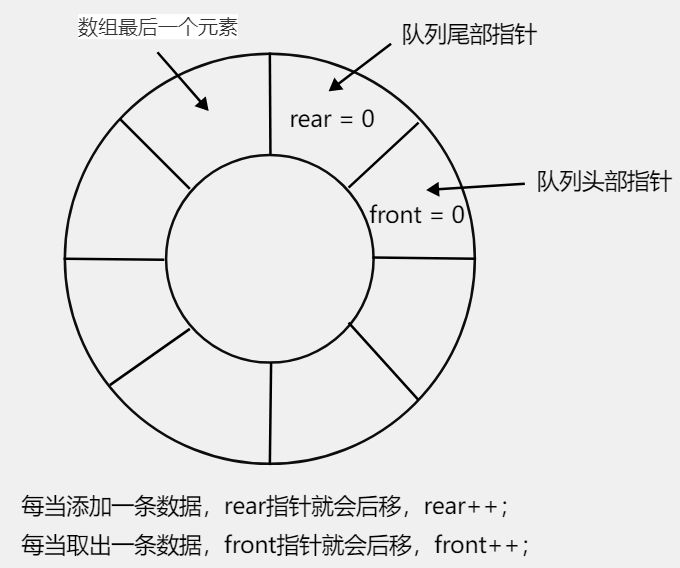
使用环形列表解决上述的问题，采用数组模拟环形队列(这个方法实际上是牺牲了一个存储单位，且最关键的部分就是取模思想)

对数组进行修改

• 将font定义为指向队列中的第一个元素queueArray[front]，其初始值为0；

• 将rear定义为指向数组最后一个元素的后一个位置，其初始值为0；

• 当队列为满时，即（rear + 1） % maxSize = front；

  • 当队列已满的时候，rear指向的这个单元是没有数据的且占用数组最后一个索引，也就是实际上rear真正值是maxSize -1

    即rear = maxSize - 1 ，当 rear + 1 = maxSize -1 +1；

    在这个情况下相当于maxSize % maxSize；试问这个情况下 结果有不为0的情况吗？front = 0；

    因此说明rear指针已经添加过一轮回到默认值的位置

  • 还看不懂的话，参考这个文章 –> 点击这里

• 当队列为空时，rear == front；

• 在这种情况下，队列的有效数据是（rear + maxSize - front）% maxSize

/**
 * @description: 使用数组模拟环形队列，解决数组模拟队列只能使用单次的问题
 */
public class QueueArray2 {
    private int front;  //队列头部指针
    private int rear; //队列尾部指针
    private int[] queueArray; //队列数组，用于存放数据
    private int maxSize; //表示数组的最大容量

    public QueueArray2() {
    }

    //创建队列的构造器
    public QueueArray2(int maxSize) {
        this.front = 0;//队列头部指针,指向队列头的第一个位置
        this.rear = 0;//队列尾部指针，指向队列中最后一个元素的后一个索引位置
        this.queueArray = new int[maxSize];
        this.maxSize = maxSize;
    }

    //判断队列是否已满
    public boolean queueIsFull(){
        return (rear + 1) % maxSize == front;
    }

    //判断队列是否为空
    public boolean queueIsEmpty(){
        return front == rear;
    }

    public int getFront() {
        return front;
    }

    //添加数据到队列中
    public void addDataInQueue(int num){
        //判断队列是否已满
        if (queueIsFull()){
            throw new RuntimeException("队列已满,无法添加数据");
        }else{
            queueArray[rear] = num;
            rear = (rear + 1) % maxSize ;
        }
    }

    //从队列中获取数据
    public int getDataFromQueue(){
        //判断队列数组是否为空
        if (queueIsEmpty()){
            //由于数组中有可能存在-1的值，故采取抛出一个异常进行提示
            throw new RuntimeException("队列没有任何数据，获取失败");
        }
        /*由于此时front指向的第一个元素
          使用一个临时变量存储取出当前指向的元素
          再将front的指针进行后移
          最后返回这个临时变量
         */
        int value = queueArray[front];
        front = (front + 1) % maxSize;
        return value;
    }

    //显示队列的所有数据
    public void showQueue(){
        if (queueIsEmpty()){
            throw new RuntimeException("队列没有任何数据");
        }else {
            for (int i = front; i < front + queueSize() ; i++) {
                /*至于为什么i要取模，例如front的数组索引为3，rear的索引为2，数组容量为5
                那么queueSize()=(2+5-3) % 5 = 4
                则i = 3 ，i < 3 + 4 (即 i < 7)，这样i的值可以取 3，4，5，6
                如果i不取模，在数组容量为5的情况下，数组就会越界
                 */
                System.out.print("queue:" + queueArray[i % maxSize] + "\n");
            }
        }
    }

    //求出队列的有效数据
    public int queueSize(){
        /*
        rear代表队列尾部的位置
        front代表队列头部的位置
        通过rear - front 就能得出有效元素，但为什么还要加上maxSize再取余，这不显得多此一举吗？
        因为这是环形队列，rear的索引值可能比front的索引值小，
        不加上maxSize再取余是有可能出现两者相减为负数的情况
         */
        return (rear + maxSize - front) % maxSize;
    }

    //显示队列的头数据(不是取出数据)
    public int showTheFirst(){
        if (queueIsEmpty()){
            throw new RuntimeException("队列没有任何数据");
        }else{
            return queueArray[front];
        }
    }
}

链表

链表的特点：

①链表是以节点的方式进行存储

②每个节点包含data域，next域(下一个节点的信息)

③链表中的各个节点在内存中不一定是连续存储的

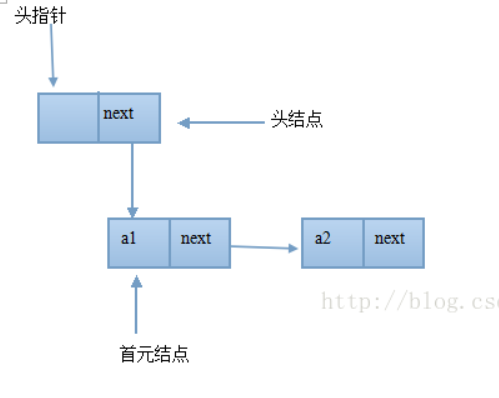
④链表分为带头节点和不带头节点的链表

• 链表可以没有头节点(通常不存储数据，仅仅指向下个节点)，

  但必须有头指针，头指针可以指向头节点或者首元节点

单向链表

单链表的缺点：只能单向查找；不能实现自我删除

(带头节点，不考虑插入节点的编号的情况下)：

//创建一个单向链表保存TestNode的节点
class SingleLinkedList{

    //创建一个头节点，不存放数据，仅指向下一个节点(首元节点)的位置
    private TestNode head = new TestNode(0,null,null);

    /**
     * Description : 添加节点并插入到单项链表的末尾
     **/
    public void add(TestNode node){
        //头节点不能动，创建一个临时指针遍历
        TestNode temp = head;
        //遍历链表
        while (true){
            //当某个节点的nextNode指向为null代表这个节点是链表的最后一个元素
            if (temp.nextNode == null) {
                break;
            }
            //没有找到则将temp指针向后移动
            else {
                temp = temp.nextNode;
            }
        }
        //退出while循环则代表找到了最后一个元素
        //将该元素的nextNode指向添加进来的元素
        temp.nextNode = node;
    }

    /**
     * Description : 显示单项链表的内容
     **/
    public void showLinkedList(){
        //首先先判断链表是否为空
        if (head.nextNode == null){
            System.out.println("当前链表为空");
            return;
        }

        //显示链表的数据
        //同理头节点不能动，创建一个临时节点
        TestNode temp = head;
        while (true){
            //判断头节点的指向的下个节点是否为空
            if (temp.nextNode != null){
                //不为空则打印这个节点的信息，并将temp指针后移
                System.out.println(temp.nextNode);
                temp = temp.nextNode;
            }else{
                //进入这个判断则代表头节点的下一个节点为空
                //没有任何数据，直接结束循环
                break;
            }
        }
    }

}

//每一个TestNode对象都是一个节点
class TestNode{
    public int num;
    public String name;
    public String nickname;
    public TestNode nextNode; //指向当前节点的下一个节点

    public TestNode() {
    }

    public TestNode(int num, String name, String nickname) {
        this.num = num;
        this.name = name;
        this.nickname = nickname;
    }
}

(带头节点，考虑插入节点的编号的情况下)：

//创建一个单向链表保存TestNode的节点
class SingleLinkedList2{

    //创建一个头节点，不存放数据，仅指向下一个节点(首元节点)的位置
    private TestNode2 head = new TestNode2(0,null,null);

    /**
     * Description : 删除链表中指定的元素
     **/
    public void delete(int node){
        //同理，头节点不能动，创建一个临时指针
        TestNode2 temp = head;
        //遍历队列
        while (true){
            //判断链表是否为空
            if (temp.nextNode == null){
                System.out.println("链表为空");
                break;
            }
            //判断下一个节点是否为要删除的节点
            else if (temp.nextNode.num == node){
                //获取被删除的节点
                TestNode2 deletedNode = temp.nextNode;
                //获取被删除节点的下一个节点
                TestNode2 DeletedNextNode = deletedNode.nextNode;
                if (DeletedNextNode != null){
                    temp.nextNode = DeletedNextNode;
                    break;
                }else {//代表删除的是最后一个节点
                    System.out.println("当前删除的是链表中最后一个节点");
                    temp.nextNode = null;
                    break;
                }
            }
            //上述的判断都都不符合
            else{
                temp = temp.nextNode;
                //判断当前temp指针是否为链表中最后一个节点
                if (temp.nextNode == null){
                    System.out.println("指定删除的节点不存在");
                    break;
                }
            }
        }

    }

    /**
     * Description : 修改链表中指定元素的值
     **/
    public void update(TestNode node){
        //同理头节点不能动，创建一个临时指针
        TestNode2 temp = head;

        //遍历链表
        while (true){
            if (temp.nextNode == null){
                System.out.println("链表为空");
                break;
            }else if (temp.nextNode.num == node.num){
                temp.nextNode.name =node.name;
                temp.nextNode.nickname =node.nickname;
                break;
            }else{
                temp = temp.nextNode;
            }
        }
    }

    /**
     * Description : 添加节点并插入到单项链表的末尾
     **/
    public void add(TestNode2 node){
        //头节点不能动，创建一个临时指针遍历
        TestNode2 temp = head;
        //遍历链表
        while (true){
            //表示链表中没有任何元素
            if (temp.nextNode == null){
                //表示链表中没有数据，会直接添加新的元素
                temp.nextNode = node;
                break;
            }
            //表示当前数据已存在
            if (temp.nextNode.num == node.num){
                System.out.println("当前添加的数据：" + node + ",已存在于链表中");
                break;
            }
            //找到元素插入的位置
            int next = temp.nextNode.num; //当前元素指向的下一个元素的位置
            int now = node.num;//新添加元素的位置
            if (now < next){
                //把新元素的下个节点的指向变成temp指向的下个节点
                node.nextNode = temp.nextNode;
                //把temp指向的下个节点变成新的元素
                temp.nextNode = node;
                break;
            }else{
                temp = temp.nextNode;
            }
        }
    }

    /**
     * Description : 显示单项链表的内容
     **/
    public void showLinkedList(){
        //首先先判断链表是否为空
        if (head.nextNode == null){
            System.out.println("当前链表为空");
            return;
        }

        //显示链表的数据
        //同理头节点不能动，创建一个临时节点
        TestNode2 temp = head;
        while (true){
            //判断头节点的指向的下个节点是否为空
            if (temp.nextNode != null){
                //不为空则打印这个节点的信息，并将temp指针后移
                System.out.println(temp.nextNode);
                temp = temp.nextNode;
            }else{
                //进入这个判断则代表头节点的下一个节点为空
                //没有任何数据，直接结束循环
                break;
            }
        }
    }

}

//每一个TestNode对象都是一个节点
class TestNode2{
    public int num;
    public String name;
    public String nickname;
    public TestNode2 nextNode; //指向当前节点的下一个节点

    public TestNode2() {
    }

    public TestNode2(int num, String name, String nickname) {
        this.num = num;
        this.name = name;
        this.nickname = nickname;
    }
}

• 几道面试题

	/**
     * Description : 百度面试题，逆序输出链表(不能破坏链表的结构)
     **/
    public static void ReservePrintLinkedList(SingleLinkedList3 reservedList){
        if (reservedList.head.nextNode == null){
            System.out.println("链表为空");
            return;
        }
        //创建一个栈，stack
        Stack<TestNode3> stack = new Stack<>();

        //遍历链表取出每一个节点放入栈中
        //创建一个临时指针
        TestNode3 temp = reservedList.head.nextNode;
        while (temp != null){
            TestNode3 curNode = reservedList.getNode(temp.num);
            stack.push(curNode);//压入栈中
            temp = temp.nextNode;
        }
        //出栈
        while (stack.size() > 0){
            System.out.println(stack.pop());
        }
    }


    /**
     * Description : 腾讯的面试题，链表的反转 就地反转解决
     **/
    public static TestNode3 reverseLinkedList2(TestNode3 headNode){
        //创建一个新的头节点
        TestNode3 newHead = new TestNode3(0,null,null);

        //链表中没有节点或者链表只有一个节点的情况
        if (headNode == null || headNode.nextNode == null){
            return headNode;
        }

        //创建临时变量分别保存前一个和后一个节点,以及一个临时指针遍历待反转的链表
        TestNode3 pre = null;
        TestNode3 next = null;
        TestNode3 temp = headNode.nextNode;

        while (temp != null){
            //分别保存当前节点的前一个和后一个节点
            next = temp.nextNode;
            pre = newHead.nextNode;
            //将新的头节点的下一个节点指向当前取出的节点
            newHead.nextNode = temp;
            //将当前节点的下一个节点指向原先新头节点指向的下一个节点
            temp.nextNode = pre;
            //将指针后移
            temp = next;
        }
        //将旧链表的下一个节点指向新的头节点的下一个节点
        return headNode.nextNode = newHead.nextNode;
    }

    /**
     * Description : 腾讯的面试题，链表的反转 头插法解决
     **/
    public static SingleLinkedList3 reverseLinkedList(SingleLinkedList3 linkedList){

        SingleLinkedList3 singleLinkedList3 = new SingleLinkedList3();
        //创建一个新的头节点
        TestNode3 newHead = singleLinkedList3.head;
        //遍历单向链表
        //头节点head不能动，创建一个临时指针
        TestNode3 temp = linkedList.head.nextNode;
        //保存当前节点的下一个节点
        TestNode3 curNext = null;

        //链表中没有节点或者链表只有一个节点的情况
        if (temp == null || temp.nextNode == null){
            return linkedList;
        }
        //开始遍历
        while (temp != null){//temp = 1
                //记录当前节点的下一个节点
                curNext = temp.nextNode;//2
                //将新的头节点与待反转链表的节点逐个相连
                temp.nextNode = newHead.nextNode;//1.next--> null
                //将新的头节点指向就待反转链表的头节点下一个
                newHead.nextNode = temp;  // 0.next --> 1
                //指针后移
                temp = curNext; //temp = temp.next
            }
            return singleLinkedList3;
    }
}

//创建一个单向链表保存TestNode的节点
class SingleLinkedList3{

    //创建一个头节点，不存放数据，仅指向下一个节点(首元节点)的位置
    public  TestNode3 head = new TestNode3(0,null,null);

    /**
     * Description : 新浪面试题，查找单链表中的倒数第k个节点
     **/
    public TestNode3 getAssignNode(int index){
        TestNode3 temp = head;
        //判断链表是否为空
        if(temp.nextNode == null){
            return null;
        }
        //获取链表中的有效节点个数
        int nodes = countList();

        //获取指定的这个index节点
        //因为temp复制的是head的地址值，所以要+1
        int num = nodes - index + 1;
        //判断要获取的index是否超过有效节点的个数
        if (num > 0 && num <= nodes){
            return getNode(num);
        }else{
            return null;
        }
    }

    /**
     * Description : 计算链表中有效节点的个数
     **/
    public int countList(){
        //不能对head头节点本身进行操作，创建一个临时变量
        TestNode3 temp = head;
        int count = 0;//记录链表中的有效节点
        while (true){
            //判断链表是否为空
            if (temp.nextNode == null){
                return count;
            }else{
                count += 1;//有效节点个数+1
                temp = temp.nextNode;//将指针移动到下一个节点，指针下移之前已经把当前这个有效节点统计了
            }
        }
    }

双向链表

特点：可以实现自我删除；双向寻找

//双向链表
class DoubleSidedLinkedList{
    public Node head = new Node(0,null,null);

    //遍历
    public void showLinkedList(){
        if (head.next == null){
            System.out.println("当前链表为空");
            return;
        }
        Node temp = head.next;
        while (temp != null){
            System.out.println(temp);
            temp = temp.next;
        }
    }

    //添加(考虑编号，按顺序添加)
    public void add(Node node){
        if (head.next == null){//链表为空，直接添加
            head.next = node;
            node.pre = head;
            return;
        }
        Node temp = head.next;
        while (true){
            if (temp.num == node.num){
                System.out.println("当前添加的节点" + node + "在链表中已存在，添加失败");
                break;
            }
            int curNum = temp.num;//当前节点的位置
            int preNum = temp.pre.num;//当前节点的上一个节点的位置
            int nodeNum = node.num;//新加入节点的位置
            //当要添加的节点的位置比当前节点的上一个节点的位置大，
            //比当前节点的位置小
            //例如双向链表是 0 --> 1 --> 4, 新添加节点位置是3时
            if (preNum < nodeNum && nodeNum < curNum){
                temp.pre.next = node;//将当前节点前一个的下一个节点指向 新添加的节点
                node.next = temp;//将新添加的节点的下一个指向 当前节点
                node.pre = temp.pre;//将新添加的节点的上一个指向 当前节点的上一个
                temp.pre = node;//将当前节点的前一个指向 新添加的节点
                break;
            }
            //当temp后的节点为空直接添加
            // 例如双向链表是 0 --> 1, 新添加节点位置是2时
            if (temp.next == null){
                temp.next = node;
                node.pre = temp;
                break;
            }else{
                temp = temp.next;
            }
        }
    }

    //修改
    public void update(Node node){
        if (head.next == null){
            System.out.println("链表为空");
            return;
        }
        Node temp = head.next;
        while (temp != null){
            if (temp.num == node.num){
                temp.name = node.name;
                temp.nickName = node.nickName;
                break;
            }else {
                temp = temp.next;
            }
        }
    }

    //删除
    public void delete(int nodeNum){
        if (head.next == null){
            System.out.println("链表为空");
            return;
        }
        Node temp = head.next;
        while (true){
            if (temp.num == nodeNum){
                //将删除节点的前一个节点的下一个节点指向被删除节点的下一个节点
                temp.pre.next = temp.next;
                //将被删除节点的后一个节点的pre节点指向被删除节点的前一个节点
                //当删除的nodeNum等于链表中最后一个节点，这一步没必要执行
                if (temp.next != null){
                    temp.next.pre = temp.pre;
                }
                break;
            }else{
                temp = temp.next;
                if (temp == null){//代表已经遍历到链表最后一个节点了
                    System.out.println("链表中不存在该节点，无法删除");
                    break;
                }
            }
        }
    }

}

//每一个node都是一个节点
class Node{
    public int num;
    public String name;
    public String nickName;
    public Node pre;//指向前一个节点
    public Node next;//指向下一个节点

    public Node() {
    }

    public Node(int num, String name, String nickName) {
        this.num = num;
        this.name = name;
        this.nickName = nickName;
    }
}

环形链表

单向环形链表应用场景：约瑟夫问题

约瑟夫问题：设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数

​ 到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，

​ 直到所有人出列为止，由此产生一个出队编号的序列。

解决思路：用一个不带头结点的循环链表来处理，先构成一个有n个结点的单循环链表（单向环形链表），

​ 然后由k结点起从1开始计数，计到m时，对应结点从链表中删除，然后再从被删除结点的下一个结点

​ 又从1开始计数，直到最后一个结点从链表中删除算法结束。

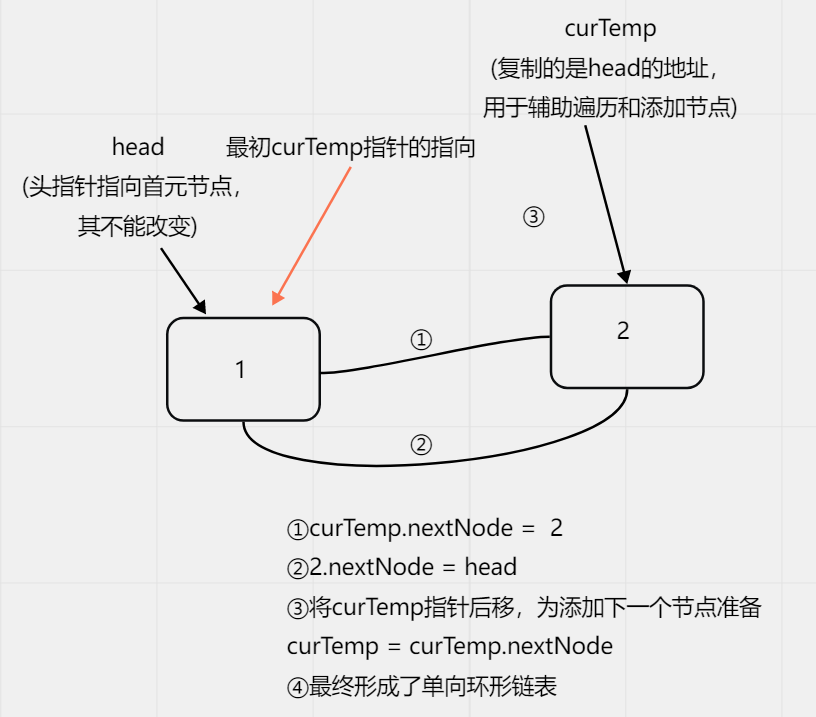
具体做法：①创建一个单向环形链表，并添加数据

​ ②将head的地址复制给一个临时指针curTemp

​ ③在进行报数时，将head和curTemp指针移动到指定位置

​ ④head指针所在位置即为需要出圈的节点，将curTemp指针的下一个节点指向head指针的下一个

​ ⑤将head指针指向其下一个节点，即为下次要开始报数的节点。

​ ⑥等head指针和curTemp指针位于同一个位置时，代表链表中只剩下一个节点，将其最终出圈

class SingleRingLinkedList{
    //创建首元节点
    public RingNode head = new RingNode(1);
    //创建临时节点，辅助遍历链表
    public RingNode curTemp = head;

    //添加环形链表
    public void add(int num){
        //最少要求一个节点
        if (num < 1){
            System.out.println("输入的节点不正确");
            return;
        }
        for (int i = 2; i <= num; i++) {
            RingNode node = new RingNode(i);
            //当链表中只有首元节点的时候(不带头节点，头指针直接指向首元节点)
            //每次添加时curTemp = curTemp.nextNode都能保证curTemp指向当前链表最后一个节点
            if (head.nextNode == null){
                head.nextNode = node;
                node.nextNode = head;
                curTemp = curTemp.nextNode;
            }else{//当链表中不止一个节点时
                curTemp.nextNode = node;
                node.nextNode = head;
                curTemp = curTemp.nextNode;
            }
        }
    }
    /**
     * Description : 约瑟夫问题解决
     * @date 2022/6/7
     * @param startNum 开始数数的节点位置
     * @param countNum 要数的次数
     * @param LinkedListNum 链表节点的个数
     * @return void
     **/
    public void JosephuQuestionResolve(int startNum,int countNum,int LinkedListNum){
        //对链表进行校验
        if (head == null || startNum < 1 || startNum > LinkedListNum){
            System.out.println("链表中没有任何节点");
            return;
        }
        //确保head指针指向要求开始的位置
        //因为开始的位置也需要报数，因此只需移动 startNum - 1
        for (int i = 1; i <= startNum - 1 ; i++) {
            head = head.nextNode;
            curTemp = curTemp.nextNode;
        }
        //遍历报数出链表
        while(true) {
            //确保head指针指向要求出圈的位置
            //因为开始的位置也需要报数，因此只需移动 countNum - 1
            for (int i = 1; i <= countNum - 1; i++) {
                head = head.nextNode;
                curTemp = curTemp.nextNode;
            }
            //打印当前出圈节点信息
            System.out.println("编号：" + head.num + "的节点出圈，" + head);
            //将curTemp的下一个节点指向被删除节点的下一个
            curTemp.nextNode = head.nextNode;
            //确保head指向下次开始的位置
            head = head.nextNode;
            if (head == curTemp) {//此时代表单向环形链表中只有一个节点
                System.out.println("链表中最后一个节点出圈，编号：" + head.num + "的节点出圈，" + head);
                break;
            }
        }
    }

    //显示环形链表
    public void showRingLinkedList(){
        if (head.nextNode == null){
            System.out.println("链表为空");
            return;
        }
        //创建一个临时指针
        RingNode temp = head;
        while (true){
            //输出当前节点
            System.out.println(temp);
            //将指针下移
            temp = temp.nextNode;
            //当temp的位置和首元节点的位置相同时代表已经遍历过了链表一次
            if(temp == head){
                break;
            }
        }
    }
}

class RingNode{
    public int num;
    public RingNode nextNode;

    public RingNode() {
    }

    public RingNode(int num) {
        this.num = num;
    }

    @Override
    public String toString() {
        return "RingNode{" +
                "num=" + num +
                '}';
    }
}

栈

概念：元素的拆入和删除只能在线性表的同一端进行操作，允许插入和删除的一端称为栈顶，另一个固定的一端称为栈底

特点：一个先进后出的有序列表

e.g：栈的应用案例

• 使用栈实现一个综合计算器

  在面对数字可能是多位数的情况下，可以考虑使用一个字符串拼接当前后面不是数字的字符

  e.g result=“ ” —> 70 —> result += index;

public class CalculatorStack {
    public static void main(String[] args) {
        //创建数字栈
        CustomizedStack numStack = new CustomizedStack(10);
        //创建符号栈
        CustomizedStack charStack = new CustomizedStack(10);

        //创建需要计算的字符串
        String string = "30*2-6*9+1";//19
        String tooMany = "";
        //将字符串转换为char型数组，并分割保存每一个字符
        char[] chars = string.toCharArray();
        //遍历每一个字符判断放入哪个栈中
        for (int i = 0; i < chars.length; i++) {
            //判断当前的字符是数字还是运算符
            if (!numStack.isCh(chars[i])){//代表是数字
                // 判断当前位置下一个是否为字符,是则直接添加进数字栈
                tooMany += chars[i];
                //说明此时i已经是最后一个字符了，不必再考虑其后面的情况，可以直接添加
                if (i == chars.length -1){
                    numStack.addData(chars[i] - 48);
                }else if (charStack.isCh(chars[i+1])){//表示当前i位置后面是运算符
                    numStack.addData(Integer.parseInt(tooMany));
                }else {//当前i的后面还是数字，跳过此次循环
                    continue;
                }
                //非常关键的一步！！！！，不清空则会影响后面的字符叠加
                tooMany = "";
            }else if (charStack.isCh(chars[i])){//代表是运算符
                //判断当前字符栈是否为空，为空则直接入栈
                if (charStack.isEmpty()){
                    charStack.addData(chars[i]);
                }else{
                    //判断操作符的优先级
                    int curPriority = charStack.charPriority(chars[i]);//当前操作符优先级
                    int ch = charStack.stackTopValue();//查看栈中操作符的值
                    int stackPriority = charStack.charPriority(ch);//栈中操作符的优先级
                    //代表当前操作符优先级比栈中操作符的优先级要低
                    if (curPriority <= stackPriority){
                        int num1 = numStack.popData();
                        int num2 = numStack.popData();
                        int c = charStack.popData();
                        int result = numStack.count(num1, num2,c);
                        //将计算结果放入数字栈中
                        numStack.addData(result);
                        //将当前操作符放入字符栈中
                        charStack.addData(chars[i]);
                    }else{
                        //将当前操作符直接放入字符栈中
                        charStack.addData(chars[i]);
                    }
                }
            }
        }

        while (true){
            if (charStack.isEmpty()){
                break;
            }
            int num1 = numStack.popData();
            int num2 = numStack.popData();
            int ch = charStack.popData();
            int result = numStack.count(num1,num2,ch);

            //将结果放入栈中
            numStack.addData(result);
            if (charStack.getTop() == -1){
                break;
            }
        }
    }
}

class CustomizedStack{
    private int arraySize;//记录数组的实际容量
    private int top = -1;//栈顶
    private int bottom = -1;//栈底
    private int[] array;//数组模拟的栈

    public CustomizedStack() {
    }

    public CustomizedStack(int arraySize) {
        this.arraySize = arraySize;
        this.array = new int[this.arraySize];
    }

    @Override
    public String toString() {
        return "CustomizedStack{" +
                "top=" + top +
                ", bottom=" + bottom + '}';
    }

    public int getTop() {
        return top;
    }

    //显示栈的数据
    public void showStack(){
        if (isEmpty()){
            System.out.println("栈中没有任何数据");
            return;
        }
        for (int i = top; i > bottom; i--){
            System.out.println(array[i]);
        }
    }

    //判断栈是否已满
    public boolean isFull(){
        //arraySize是数组最大容量
        //当top = arraySize - 1代表已经添加到数组最后一个位置，
        //此时栈已满
        return top >= arraySize - 1;
    }

    //判断栈是否为空
    public boolean isEmpty(){
        //top默认为-1，-1处没有元素
        return top == -1;
    }

    //入栈
    public void addData(int num){
        if (isFull()){
            System.out.println("栈已满，添加失败");
            return;
        }
        //top++;；
        top++;
        //给数组中top位置赋值
        array[top] = num;
    }

    //出栈
    public int popData(){
        if (isEmpty()){
            System.out.println("栈中没有任何数据");
            return -2;
        }
        //先把数组中top位置的数值返回，再将top指针-1，调整栈的元素
        return array[top--];
    }

    //判断运算字符的优先级,数字越大优先级越高
    public int charPriority(int ch){
        if (ch == '*' || ch == '/'){
            return 1;
        }else if (ch == '+' || ch == '-'){
            return 0;
        }else{
            return -1;
        }
    }

    //判断是否为一个运算符,返回true则代表是运算符，否则则代表为数字
    public boolean isCh(char ch){
        return ch == '*' || ch == '/' || ch == '-'|| ch == '+';
    }

    //进行运算
    public int count(int num1,int num2,int ch){
        int result = 0;//储存最终的计算结果
        switch (ch){
            case '+':
                result = num1 + num2;
                break;
            case '-':
                //经过推算，无论是num2>num1或num2<num1的情况都适用
                result = num2 - num1;
                break;
            case '*':
                result = num2 * num1;
                break;
            case '/':
                result = num2 / num1;
                break;
        }
        return result;

    }

    //查看当前栈的栈顶值
    public int stackTopValue(){
        return array[top];
    }
}

• 后缀表达式的计算

//逆波兰表达式
public class InversePolandNotation {
    public static void main(String[] args) {
        String suffixExpression = "4 5 * 8 - 60 + 8 2 / +";

        //将这个后缀转换为数组
        String[] array = suffixExpression.split(" ");
        int result = InversePolandNotation.ReversePolishNotationCount(array);
        System.out.println("后缀表达式的结果是：" + result);

    //计算当前的逆波兰表达式的值
    public static int ReversePolishNotationCount(String[] array){
        if (array.length == 0){
            throw new RuntimeException("传入的数组为空");
        }
        int result = 0;
        Stack<String> stack = new Stack<>();
        for (int i = 0; i < array.length; i++) {
            if (array[i].matches("\\d+")){//匹配的是多位数
                stack.push(array[i]);//将当前字符压入栈中
            }else{
                int num1 = Integer.parseInt(stack.pop());
                int num2 = Integer.parseInt(stack.pop());
                if ("+".equals(array[i])){
                    result = num2 + num1;
                }else if ("-".equals(array[i])){
                    result = num2 - num1;
                }else if ("*".equals(array[i])){
                    result = num2 * num1;
                }else if ("/".equals(array[i])){
                    result = num2 / num1;
                }else{
                    throw new RuntimeException("当前字符不合法");
                }
                //将计算得到的结果入栈
                stack.push(String.valueOf(result));
            }
        }
        return result;//返回计算结果
    }
    }	

三种不同的表达式 —> 表达式互转的理解

• 前缀表达式

前缀表达式又称波兰表达式

特点：前缀表达式都以运算符开头，以操作数结尾，前缀表达式在计算机的求值中是从右至左进行扫描

e.g：中缀表达式的(3+4)*5-6 对应的前缀表达式是 - * + 3 4 5 6

• 中缀表达式

中缀表达式是最熟悉和常见的计算表达式，中缀表达式通常有小括号

• 后缀表达式

后缀表达式又称逆波兰表达式

特点：后缀表达式都以操作数开头，以运算符结尾，后缀表达式在计算机的求值中是从左至右进行扫描

e.g：中缀表达式的(3+4)*5-6 对应的后缀表达式是 3 4 + 5 * 6 -

中缀表达式转后缀表达式思路及代码示例

/**
以下解决思路只是选择使用一个栈和一个集合相互辅助解决实现从
中缀表达式到后缀表达式的实现以及后缀表达式的计算结果
- 具体使用两个栈来完成的写在工程中package stack包的InversePolandNotation类中;
*/	
//计算当前的逆波兰表达式的值
public static int ReversePolishNotationCount(String[] array){
    if (array.length == 0){
        throw new RuntimeException("传入的数组为空");
    }
    int result = 0;
    Stack<String> stack = new Stack<>();
    for (int i = 0; i < array.length; i++) {
        if (array[i].matches("\\d+")){//匹配的是多位数
            stack.push(array[i]);
        }else{
            int num1 = Integer.parseInt(stack.pop());
            int num2 = Integer.parseInt(stack.pop());
            if ("+".equals(array[i])){
                result = num2 + num1;
            }else if ("-".equals(array[i])){
                result = num2 - num1;
            }else if ("*".equals(array[i])){
                result = num2 * num1;
            }else if ("/".equals(array[i])){
                result = num2 / num1;
            }else{
                throw new RuntimeException("当前字符不合法");
            }

            //将计算得到的结果入栈
            stack.push(String.valueOf(result));
        }
    }
    return result;
}

//将输入的中缀表达式各个符号逐个分割
public static List inFixExpression(String expression){
    if ("".equals(expression)){
        throw new RuntimeException("表达式为空");
    }
    List<String> list = new ArrayList<>();//用于储存扫描后的中缀表达式
    String string = "";//用于拼接字符串

    //将字符串变为数组以便于遍历
    char[] array = expression.toCharArray();
    for (int i = 0; i < array.length; i++) {
        //i == 数组最后一个元素则直接添加即可
        if (i == array.length - 1){
            list.add(String.valueOf(array[i]));
            break;
        }
        //判断是否为符号
        if (InversePolandNotation2.isCh(array[i])){
            list.add(String.valueOf(array[i]));
        }else{
            //判断此位置后面是否还是数字
            string += String.valueOf(array[i]);
            if (!InversePolandNotation2.isCh(array[i+1])){
                continue;
            }else{
                list.add(string);
            }
        }
        string = "";
    }
    return list;
}

//将中缀表达式转换为后缀表达式
public static List<String> inFixToSuffixExpression(List<String> list){
    //将传入的list集合转为string数组便于遍历
    String[] inFix = list.toArray(new String[0]);

    //创建一个集合和一个栈用于存储运算符和数字
    List<String> suffixList = new ArrayList<>();//最终的后缀表达式
    Stack<String> charStack = new Stack<>();//放运算符

    //遍历转换后中的集合的数组
    for (int i = 0; i < inFix.length; i++) {
        if (!inFix[i].matches("\\d+")){//属于字符
            while (true){
                //如果当前字符栈为空,或当操作符和栈顶操作符相同且都是左括号（时,
                //可用直接将当前字符添加入字符栈中
                if (charStack.empty() || array[i] == charStack.peek() && charStack.peek() == '('){
                    charStack.push(array[i]);
                    break;
                }
                //又或者是左括号（时也可以直接添加入符号栈
                else if (array[i] == '('){
                    charStack.push(array[i]);
                    break;
                }
                //如果当前字符为)右括号，则需要将符合栈中的运算符弹出压入数字栈
                // ，直至遇到(左括号
                else if (array[i] == ')'){
                    while (charStack.peek() != '('){
                        //弹出符号栈栈顶元素
                        Character first = charStack.pop();
                        //压入数字栈中
                        numStack.push(first);
                    }
                    //将当前的(出栈
                    charStack.pop();
                    break;
                } else{//不为空
                    Character top = charStack.peek();//查看栈顶的值
                    int topLevel = InversePolandNotation.charPriority(top);
                    int curLevel = InversePolandNotation.charPriority(array[i]);
                    //栈顶运算比当前运算符优先级低
                    if (curLevel > topLevel){//当前操作符等级更高，直接入栈
                        charStack.push(array[i]);
                        break;
                    }else{//当前操作符等级比栈顶运算符等级低
                        Character c1 = charStack.pop();//弹出符号栈栈顶元素
                        numStack.push(c1);//将被弹出的运算符压入数字栈中
                        charStack.push(array[i]);//将当前运算符加入到符号栈
                        break; //必须结束循环，否则会出现死循环
                    }
                }
            }
        }else{//属于数字
            suffixList.add(inFix[i]);
        }
    }
    //将字符栈的元素逐个弹出压入用于存储后缀表达式的集合中
    while (!charStack.empty()){
        String theEnd = charStack.pop();
        suffixList.add(theEnd);
    }
    //返回这个集合
    return suffixList;
}

//判断是否为一个运算符,返回true则代表是运算符，否则则代表为数字
public static boolean isCh(char ch){
    return ch == '*' || ch == '/' || ch == '-'|| ch == '+' || ch == '(' ||ch == ')';
}

//判断运算字符的优先级,数字越大优先级越高
public static int charPriority(String ch){
    if ("*".equals(ch) ||"/".equals(ch)){
        return 1;
    }else if ("+".equals(ch) ||"-".equals(ch)){
        return 0;
    }else if ("(".equals(ch) ||")".equals(ch)){
        return -1;
    }else {
        return -2;
    }
}

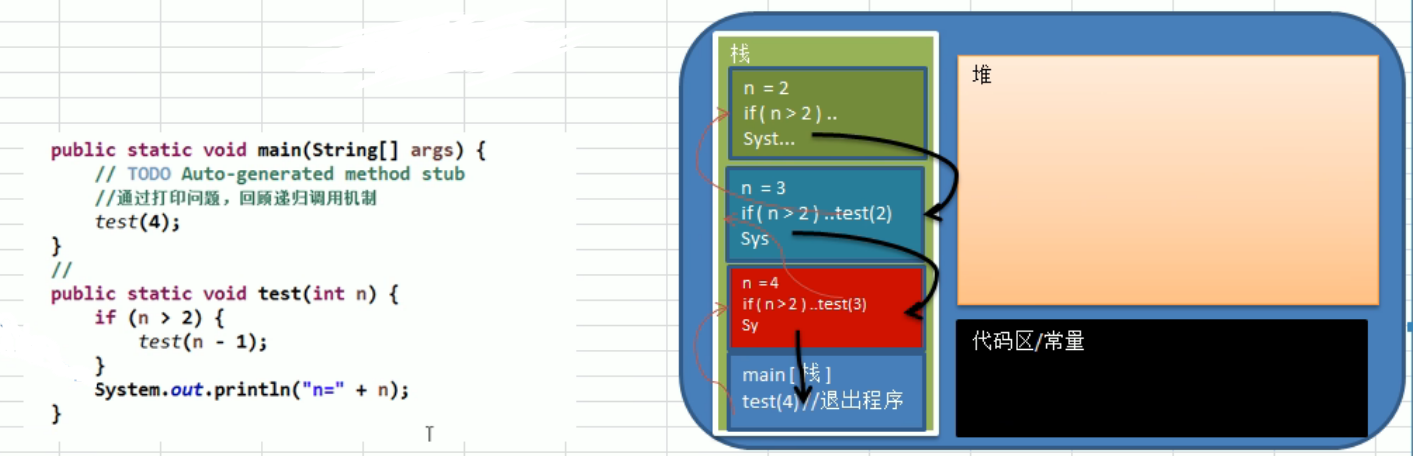
递归

递归调用规则：

①当程序执行到一个方法时，就会开辟一个独立的空间(栈)

②每个空间的数据(局部变量)，都是独立的

• 但是如果方法中的形参使用的引用数据类型，则所有方法使用的都是该引用数据类型的变量

③递归必须是有方向的，也就是必须向退出递归的方向进行

④当方法执行完毕，或者遇到return就会返回，遵循谁调用返回给谁的原则。

• 迷宫回溯问题

public class MiGongTest {
    public static void main(String[] args) {
        //创建一个二维数组用于代表地图
        int[][] map = new int[8][7];

        //使用1表示墙
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                if (i == 0 || j == 0 || i == map.length-1 || j == 6){
                    map[i][j] = 1;
                }else if (i == 3 && j == 1 || i == 3 && j == 2){
                    map[i][j] = 1;
                } else {
                    map[i][j] = 0;
                }
            }
        }
}

    /**
     * Description : 判断是否可以走通
     * 必须要考虑清楚小球是从哪个位置开始，又是到哪个位置就表示结束
     * 0表示没有走过，1表示墙，2表示走过的，3表示已经走过，但走不通，map[6][5]代表已经达到地图出口
     * 按照小球的移动策略是从下-->右-->上-->左-->
     * @date 2022/6/13
     * @param map 表示地图
     * @param i 表示从地图哪一行开始找
     * @param j 表示从地图哪一列开始找
     * @return boolean
     **/
    public static boolean isFindWay(int[][] map,int i,int j){
        if (map[6][5] == 2){//表示已达到出口
            return true;
        }else{
            if (map[i][j] == 0){//代表这个点还没走过
                map[i][j] = 2;//假设这个点是可以走过的
                /*
                能够进入递归方法代表此点可走，返回了true，否则就是返回false，
                然后就去不断的进入别的else if语句中的递归方法，周而复始。
                一旦发现某个点四个方向都走不通，就会回溯到上一个递归方法，
                继续执行这些步骤，直至回到第一个递归方法，如果发现也是全部
                走不通，返回最终结果false
                 */
                if (isFindWay(map,i+1,j)){//先尝试往下左
                    return true;
                }else if (isFindWay(map,i,j+1)){//尝试往右走
                    return true;
                }else if (isFindWay(map,i-1,j)){//尝试往上走
                    return true;
                }else if (isFindWay(map,i,j-1)){//尝试往左走
                    return true;
                }else{
                    /*
                    当进入这个方法代表上面的所有方向全部走不通，
                    要将之前假定此点能走通设置的2重新置为3并返回false
                     */
                    map[i][j] = 3;
                    return false;
                }
            }else{//当map[i][j] != 0时，可能是1，2，3
                return false;
            }
          }
        }
}

• 八皇后问题

  

  使用一个一维数组记录所有皇后成功放置的位置

  例如 array[8] = {0,4,7,5,2,6,1,3} 数组下标表示皇后在第几行，数组下标对应的值表示皇后在第几列

  for是水平移动皇后,递归是继续摆下一个皇后,回溯是回到上一行

public class QueenRecursion {

    //定义皇后的最大数量
    int max = 8;

    //定义一个数组保存八个皇后都能正确放置的位置
    int[] queenArray = new int[max];
    static int count = 0;
    public static void main(String[] args) {
        QueenRecursion queenRecursion = new QueenRecursion();
        queenRecursion.check(0);
        System.out.println("result：" + count);

    }

    /**
     * Description : 添加皇后
     * 需要注意的是check方法每一次递归时，进入到check中都会有一个for循环,
     * 等获取到一个完整解就会返回上一个栈，也就是上一个for循环继续在同一行
     * 尝试将皇后摆在下一列，判断是否为另一个完整解释
     * i --> 控制第几列，queenArray[i]的值控制第几行
     * @date 2022/6/14
     * @param n 第n+1个皇后
     * @return void
     **/
    private  void check(int n){
        if (n == max){//当n等于8时，实际上是在添加第9个皇后
            //代表已经得到一条八皇后摆放的正确解，进行打印
            showQueenArray();
            return;
        }
        for (int i = 0; i < max; i++) {
            //先放第一个皇后，先放在该行的第一列
            queenArray[n] = i;
            //判断放到第n个皇后到i列时，是否冲突
            if (judge(n)){
                //进入此结构代表不冲突，可以接着往下放n+1个皇后，开始递归
                check(n+1);
            }
            //如果发生冲突，则会放到本行的下一列进行重新比较，
            //因为这里的下一列是由i控制的，因此会自动往下一列放
        }
    }

    /**
     * Description : 判断已经放置的皇后是否和之前放置的有冲突
     * @date 2022/6/14
     * @param n 表示第n+1个皇后
     * @return boolean
     **/
    private boolean judge(int n){
        for (int i = 0; i < n; i++) {
            /* 皇后摆放位置要求：
            1.不能在同一列
            2.当行差和列差相等时则表示两个皇后在同一个斜线上，因此行差和列差不能相等
            3.不能在同一行，但因为这里使用了一维数组代替二维数组，本身n是不断变化的，
              摆完一个皇后自动换下一行，因此这里不可能会在同一行，也就不需要判断
             */
            if (queenArray[i] == queenArray[n] || Math.abs(n-i) == Math.abs(queenArray[n] - queenArray[i])){
                return false;
            }
        }
        return true;
    }

    private  void showQueenArray(){
        for (int i = 0; i < queenArray.length; i++) {
            System.out.print(queenArray[i] + "\t");
        }
        count += 1;
        System.out.println();
    }
}

• 递归和回溯的区别

①递归是一种算法结构，回溯是一种算法思想,回溯法是用递归实现

②递归的定义：通常来说，为了描述问题的某一状态，必须用到该状态的上一个状态；而如果要

描述上一个状态，又必须用到上一个状态的上一个状态…… 这样用自己来定义自己的方法就是递归。

回溯的定义：回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，

发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法。

③回溯算法其实是一种试探，该方法放弃关于问题规模大小的限制，并将问题的方案按某种顺序逐一

枚举和试验。发现当前方案不可能有解时，就选择下一个方案，倘若当前方案不满足问题的要求时，

继续扩大当前方案的规模，并继续试探。如果当前方案满足所有要求时，该方案就是问题的一个解。

放弃当前方案，寻找下一介方案的过程称为回溯。 而递归算法依赖与前一步的结果，它的结果来源于

一条主线，是确定的，而不是试探的结果，这就是其与回溯的区别，而在很多情况下，回溯与递归算法

是在一起使用的。

举个其他博主的提供例子：我们在路上走着，前面是一个多岔路口，因为我们并不知道应该走哪条路，

所以我们需要尝试。尝试的过程就是一个函数。我们选择了一个方向，后来发现又有一个多岔路口，

这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上，再做一次尝试，即在函数内部

再调用一次函数，这就是递归的过程。这样重复了若干次之后，发现这次选择的这条路走不通，这时候

我们知道我们上一个路口选错了，所以我们要回到上一个路口重新选择其他路，这就是回溯的思想。

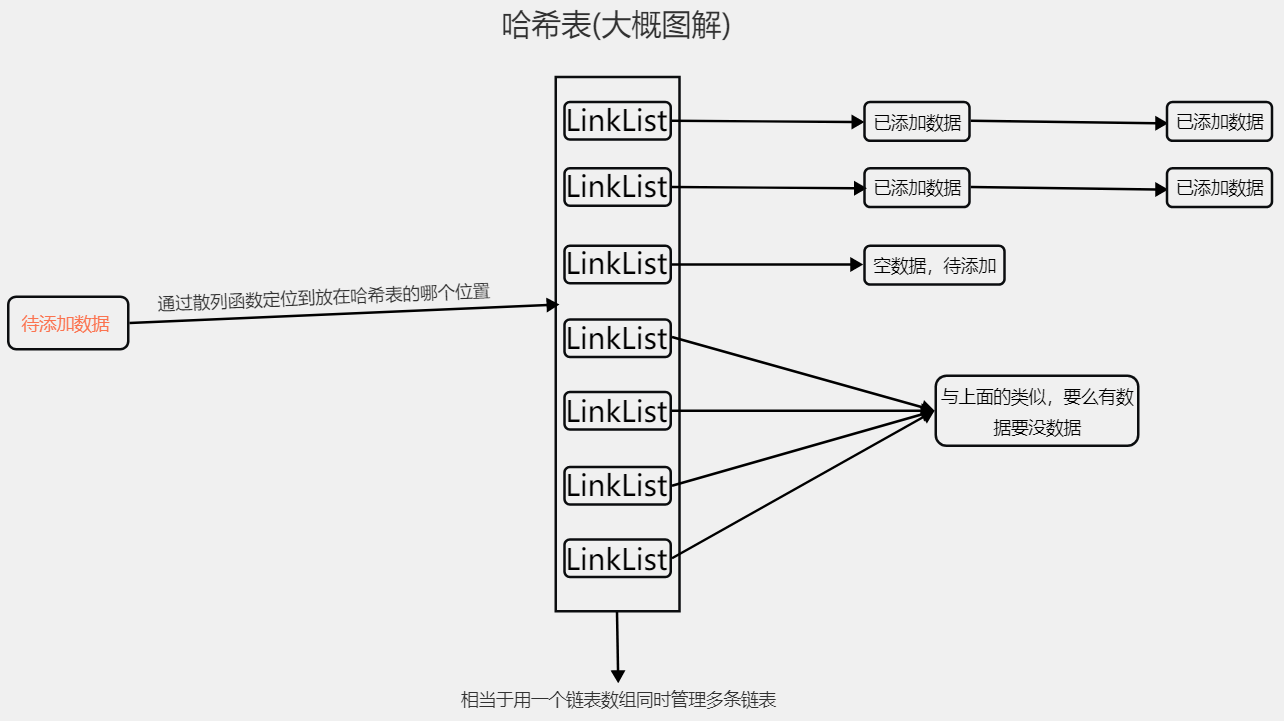
哈希表

散列表（Hash table，也叫哈希表）：根据关键码值(Key value)而直接进行访问的数据结构。

它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。

这个映射函数叫做散列函数，存放记录的数组叫做散列表。

public class EmpLinkList {
    //相当于头指针，直接指向第一个emp对象，默认为null
    //可以理解为把第一个emp对象当作了头指针
    private Employee headEmp;
}
//哈希表，通过链表数组管理多个员工类链表
public class MyHashTable {
    private static EmpLinkList[] empLinkListArray;
    private static int arrSize;

    public MyHashTable(int size) {
        arrSize = size;
        empLinkListArray = new EmpLinkList[size];//初始化链表数组
        //由于创建的是对象数组，默认对象都是null，则必须对数组的各个元素进行初始化
        for (int i = 0; i < empLinkListArray.length; i++) {
            empLinkListArray[i] = new EmpLinkList();
        }
    }
    
    /**
     * Description : 散列函数，确认当前id应该放在
     * @param id 当前员工id
     **/
    public int hashMethod(int id){
        return id % arrSize;
    }
}

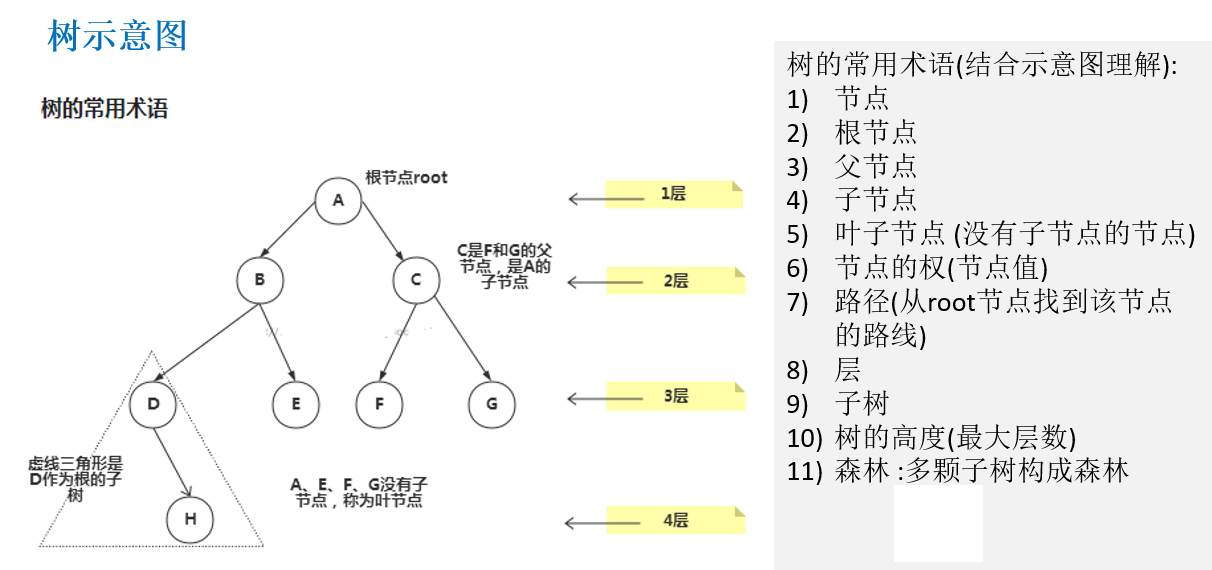
树结构

概念

• 使用树的优势

数组在对于查找的效率很快，对于频繁的插入和删除效率较低

链表对频繁的插入和删除效率较高，但对于查找的效率较低

树既能提高数据的查找读取的效率，同时也能保证数据的插入、删除、修改的速度。

• 树图解

无序二叉树

二叉树：每个节点最多只能有两个子节点。二叉树的子节点分为左节点和右节点。

满二叉树：所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数

完全二叉树：所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，

倒数第二层的叶子节点在右边连续。若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的

结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边。

遍历

• 前序、中序、后序遍历

前序遍历：先遍历根结点，再遍历左子树，最后遍历右子树

中序遍历：先遍历左子树，再遍历根结点，最后遍历右子树

后序遍历：先遍历左子树，再遍历右子树，最后遍历根结点

所谓前序、中序、后序遍历就是就是针对根节点所在的位置而言的。

代码过长，具体到DataStucture目录下的tree包下查看

查找

基本就是在遍历的基础上进行的，只需要将打印语句换成判断条件并返回查找到的节点即可

删除

具体思路：1.先判断当前删除的是不是root根节点，是的话直接置空root整个树

​ 2.不是根节点的话，先判断删除的是否为根节点的左子节点或根节点的右子节点

​ 3.如果都不是，就先开始向左递归查找对应节点

​ 4.如果左边递归找不到，再开始向右递归查找对应节点

/**
* Description : 删除指定id的二叉树节点
* 由于这个二叉树是一个单向的，因此不能去判断当前节点是否为需要删除的节点
* 因为无法通过当前节点找到其父节点去修改指向，其实就是单向链表删除的思路
* @param id 待删除的节点id
**/
public void deleteNode(int id){
    //由于root在一开始就判断过了，因此能进来的节点必不可能是root节点
    //假设root = 1
    HeroNode leftNode = this.getLeft();//2
    HeroNode rightNode = this.getRight();//3
    //不为空左子节点或者右子节点才能进入
    if (leftNode != null && rightNode != null) {
        //判断左子节点是否为需要删除的节点
        if (leftNode.getId() == id){
            //删除此相等的节点
            this.setLeft(null);
            return;//置空后立即结束，停止递归
        }
        //判断右子节点是否为需要删除的节点
        if (rightNode.getId() == id){
            //删除此相等的节点
            this.setRight(null);
            return;//置空后立即结束，停止递归
        }
    }
    //向左递归遍历寻找
    if (this.getLeft() != null){
        this.getLeft().deleteNode(id);
    }
    //向右递归遍历寻找
    if (this.getRight() != null){
        this.getRight().deleteNode(id);
    }
}

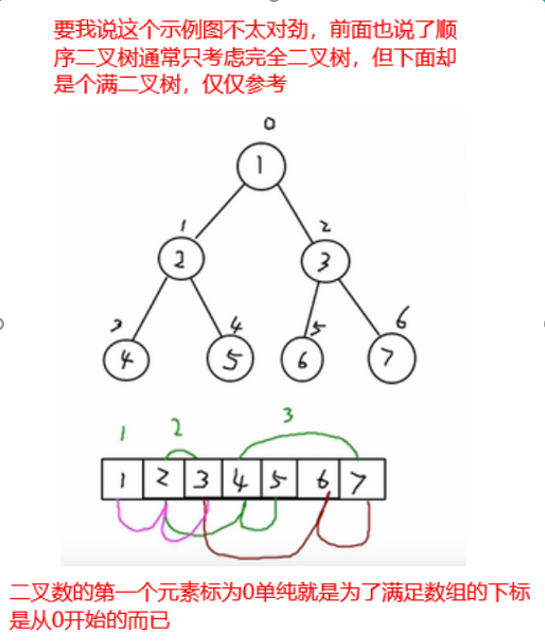
顺序存储二叉树

• 什么是顺序存储

顺序存储，指的是连续的空间如数组方式存储树的节点

• 顺序存储二叉树解决了什么问题？

数组存储方式和树的存储方式可以相互转换，数组可以转换成树，树也可以转换成数组

• 顺序存储二叉树的特点

①顺序二叉树通常只考虑完全二叉树

②第n个元素的左子节点为 2 * n + 1

③第n个元素的右子节点为 2 * n + 2

④第n个元素的父节点为 (n-1) / 2

n : 表示二叉树中的第几个元素(按0开始编号如图所示)；实际上n也对应这元素在数组中的下标

• 代码示例仅仅放了前序遍历，完整的前序、中序、后序放在了tree.arraybinarytree包下

  其实前序、中序、后序无非就是改变了打印当前节点的位置

/**
     * Description : 以数组的方式遍历完成前序遍历
     * @param index 传入的下标值
     **/
public void preOrder(int index){
    if (array == null || array.length == 0){
        System.out.println("数组为空不能执行前序遍历");
        return;
    }
    //输出当前数
    System.out.println(array[index]);
    //搜索左子节点的位置并向左执行递归遍历
    int left = 2*index+1;
    if (left < array.length){
        preOrder(left);
    }

    //搜索右子节点的位置并向右执行递归遍历
    int right = 2*index+2;
    if (right < array.length){
        preOrder(right);
    }
}

线索二叉树

• 什么是线索二叉树

公式n+1的推导：当有n个节点时，每个节点有两个指针，即总共可用指针为2n

但是除了根节点以外，其他节点头上都有一条指针指向它，因此需要n-1个指针

例如6个节点，你会发现总共有5个节点头上有指针连接

所以剩余可用指针(即为空指针)为 2n-(n-1) ==> n+1

线索二叉树(Threaded BinaryTree)：n个结点的二叉链表中含有n+1个空指针域。利用二叉链表中的空指针域，

存放指向该结点在某种遍历次序下的前驱和后继结点的指针（这种附加的指针称为”线索”）。而加上了线索的

二叉链表称为线索链表，相应的二叉树称为线索二叉树。

前驱结点：一个结点的前一个结点 后继结点：一个结点的后一个结点

• 线索二叉树的分类

根据线索性质的不同，可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种

• 线索二叉树解决了什么问题？

在完全二叉树的情况下，叶子节点和某些子树节点的左右指针没有完全利用上，

通过线索二叉树能够充分利用各个节点的左右指针

• 中序线索化二叉树的思路

实际就是先通过左边中序遍历查找到最左边的叶子节点，再判断一下此叶子节点左右指针是否需要线索化，

如何左右都需要线索化，则先只线索化左边指针，让其指向前驱节点(没有前驱节点则为null)，因为此叶子节点

是第一个被遍历的，它前面没有其他节点了。至于右边的指针，则留到下一个节点判断左右指针线索化的时候

完成(但前提是需要使用一个外界公共属性保存各个节点的上一个节点，便于后继节点的指向，这个属性的值

不能随着压栈操作的结束而消失,否则线索化会失败)。并将这个公共属性的值修改为当前节点值。最后才进行

线索化右边指针，当这个公共属性不为空且它的右指针为空时代表就是上个未进行右指针线索化的节点。

/**
     * Description : 中序二叉树转为中序线索二叉树
     * @param node 当前遍历的节点
     **/
public void midThreadedBinaryTreeTest(HeroNode node){//1
    //为空不可线索化，递归结束的条件
    if (node == null){
        return;
    }

    //1.对左子树线索化
    midThreadedBinaryTreeTest(node.getLeft());
    /*2.对中间数线索化
            当从上面的递归方法来到这步，则代表遍历到最左边的叶子节点了
             */
    if (node.getLeft() == null){
        //线索化左边指针
        node.setLeft(ThreadedBinaryTree.pre);
        node.setLeftType(true);
    }

    /*
     ThreadedBinaryTree.pre是定义在别的类中保存当前节点的上一个节点的静态属性，
     让其值不会随着栈的压栈操作结束消失。
     当这个公共属性不为空且它的右指针为空时代表就是上个未进行右指针线索化的节点。
    */
    if (ThreadedBinaryTree.pre != null && ThreadedBinaryTree.pre.getRight() == null){
        //线索化上个节点尚未完成的右指针
        ThreadedBinaryTree.pre.setRight(node);
        ThreadedBinaryTree.pre.setRightType(true);

    }
    /* 
            这一步很重要，让pre属性能够动态保存多个节点的对应的自己的上个节点，
            缺少这步线索化直接失败
             */
    ThreadedBinaryTree.pre = node;

    //3.对右子树线索化
    midThreadedBinaryTreeTest(node.getRight());
}

• 中序线索二叉树的遍历思路

因为线索化的二叉树不能再使用之前的遍历方式，因此在节点中添加了leftType和rightType属性

表示是指向前驱、后继节点还是左、右子树，中序是先从左子树开始的，而线索二叉树的第一个

元素有一个最明显的特征，即其的leftType属性必然是true，从而找到左子树最底层的叶子节点，

由于后继节点表示一个节点的下一个节点，因此可以通过循环比较节点的rightType属性，如果

是true代表指向其后继节点，可以直接输出该节点，如果false，表示其指向其子树，则跳出循环，

用当前不是指向后继节点的节点替代原来的node，继续重复上面的步骤，直至找到一个为null的

节点，最终结束遍历

public static void showThreadedBinaryTree(HeroNode node){
    while (node != null){
        //先找到第一个左边指针指向前驱节点的元素，此节点的leftType属性被定义为了true
        while (!node.leftType){
            node = node.getLeft();
        }
        System.out.println(node);
        /*
            node.rightType表示当前节点的右指针指向其后继节点，
            后继节点表示为当前节点的下一个节点
             */
        while (node.rightType){
            node = node.getRight();
            System.out.println(node);
        }
        //当从上面循环出来，代表此时n当前节点的右指针指向其子树
        //用当前节点的右子树节点代替当前节点继续判断
        node = node.getRight();
    }
}

赫夫曼树

赫夫曼树(哈夫曼树)：即给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)

最小，称这样的二叉树为最优二叉树，赫夫曼树是带权路径长度最短的树，权值越大的结点离根越近

路径：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。

路径长度：通路中分支的数目称为路径长度，若根结点的层数为1，则从根结点到第L层结点的路径长度为L-1

结点的权：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积

树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL(weighted path length) 。

• 构建赫夫曼树思路

1.将无序序列从小到大进行排序, 将每一个数据看成一个节点 ， 而每个节点又看成是一颗最简单的二叉树(左右节点为空)

2.取出当前前两个根节点权值较小的二叉树

3.组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗根节点权值较小的二叉树之和

再设置此二叉树的左右节点，最后将这颗新的二叉树加入序列，以根节点的权值大小再次进行排序

4.不断重复 1-2-3 的步骤，直到数列中，所有的数据都被处理，此时就得到一颗赫夫曼树

(此处案例以集合来表示各个二叉树，当所有数据被处理后，集合中仅剩一个元素，此元素就是赫夫曼数的根节点)

public static Node createHuffManTree(int[] array){
    List<Node> nodes = new ArrayList<>();
    for (int i: array){
        nodes.add(new Node(i));
    }
    //以集合来表示各个二叉树，每个元素都是一个二叉树
    Collections.sort(nodes);

    while (nodes.size() > 1){
        //取出集合中的前两个元素(即两个二叉树)
        Node leftNode = nodes.get(0);
        Node rightNode = nodes.get(1);

        //进行构建新的二叉树
        Node parent = new Node(leftNode.value + rightNode.value);
        //设置当前二叉树的左右节点
        parent.left = leftNode;
        parent.right = rightNode;

        //移除取出的二叉树
        nodes.remove(leftNode);
        nodes.remove(rightNode);

        //将新构建的二叉树加入集合并对集合内的对象元素重新排序
        nodes.add(parent);
        Collections.sort(nodes);
    }
    /*
        当从上面的循环中出来，此时集合中只有最终的一个根节点，
        因为在取出数据构成新二叉树后又进行了对原先取出数据的删除操作，
        再加入了新构建的节点(二叉树)
         */
    return nodes.get(0);
}

二叉排序树

• 二叉排序树Binary Sort(Search) Tree)

任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大。

如果有相同的值，可以将该节点放在左子节点或右子节点

• 简单缕缕二叉排序树的删除思路

得先判断当前待删除的节点是否存在，再得考虑这三种情况：

1.当前待删除的节点为叶子节点

叶子节点为父节点的左子节点 或 叶子节点为父节点的右子节点

2.当前待删除的节点只有一个子树(只有左子树或右子树)

待删除节点是父节点的左节点，待删除节点有个左节点

待删除节点是父节点的左节点，待删除节点有个右节点

待删除节点是父节点的右节点，待删除节点有个左节点

待删除节点是父节点的右节点，待删除节点有个右节点

3.当前待删除的节点有两个子树

两种方法：①则需要找到父节点的右子树的最小值，因为右子树的最小值比左子树的所有值都要大)

②需要找到待删除节点的左子树的最大值，因为左子树的最大值比右子树的所有值都要小)

具体代码到tree.binarysorttree包下查看

平衡二叉树

• 什么是平衡二叉树

平衡二叉树是基于二叉排序树的基础上出现的，也叫平衡二叉搜索树（Self-balancing binary search tree）

又被称为AVL树， 可以保证查询效率较高。

• 平衡二叉树的特点

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

• 为什么需要平衡二叉树

在通过一个有序的数组[1,2,3,4,5,6,7,8]创建一个二叉树会出现此树左子树都为空，整个二叉树表现得像个

单向链表，虽然插入速度不受影响，但查询效率大大减低，因为每次都需要比较左子树。

• LL失衡(右单旋转)

当前二叉树的左子树与右子树高度差大于1，需要向右旋转，降低左子树高度

• RR失衡 (左单旋转)

当前二叉树的右子树与左子树高度差大于1，需要向左旋转，降低右子树高度

• 双旋转(在某些情况下，仅仅单向左右旋转并不能将非平衡二叉树转为平衡二叉树)

  • LR失衡(先左旋转再右旋转)

    ①当前二叉树符合需要右旋转的情况

    ②当前节点的左节点的右子树高度大于当前节点的左节点的左子树高度

    ③将当前节点的左节点进行左旋转

    ④再将当前节点进行右旋转

  • RL失衡(先右旋转再左旋转)

    ①当前二叉树符合需要左旋转的情况

    ②当前节点的左节点的右子树高度大于当前节点的左节点的左子树高度

    ③将当前节点的左节点进行左旋转

    ④再将当前节点进行右旋转

具体代码到tree.avl包下查看

多路查找树

• 什么是多路查找树（multiway tree）

多路查找树也称为多叉树，它允许每个节点可以有更多的数据项和更多的子节点

• 多路查找树出现的背景

二叉树需要从数据库或者磁盘中加载到内存，如果二叉树的节点过多就会导致I/O操作频繁，且普通二叉树的节点

过多会极大降低操作效率。

节点度：当前节点下的所有子节点的个数

树的度：所有节点度的最大值

2-3树

• 什么是2-3树

2-3树是由二节点和三节点构成的树。2-3树是最简单的B树，且2-3树依旧具有二叉排序树的要求

• 2-3树的特点

  • 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
  • 有两个子节点的节点叫二节点，二节点要么没有子节点，要么有两个子节点.
  • 有三个子节点的节点叫三节点，三节点要么没有子节点，要么有三个子节点.

• 插入规则

当按照2-3树的特点插入一个数到某个节点时，不能满足上面三个要求，就需要拆，先向上拆，

如果上层满，则拆本层，拆后仍然需要满足上面3个条件。对于三节点的子树的值大小仍然遵守

(BST 二叉排序树)的规则

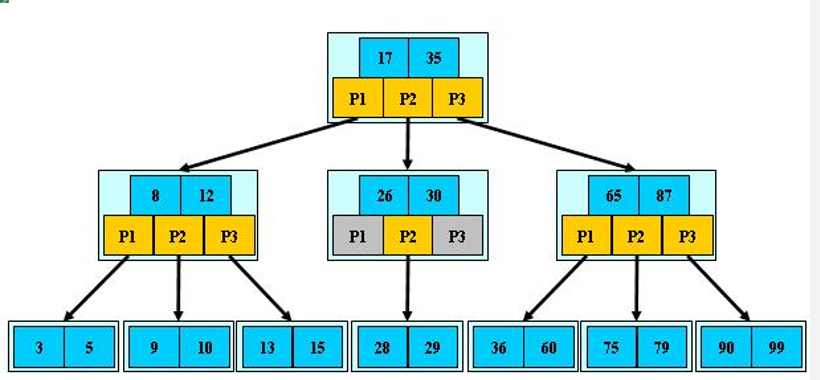
B树

B-tree树即B树，B即Balanced，平衡的意思。

• B树的特点(其搜索性能等价于在关键字全集内做一次二分查找)

①B树的阶：节点的最多子节点个数。比如2-3树的阶是3，2-3-4树的阶是4

②B-树的搜索：从根结点开始，对结点内的关键字（有序）序列进行二分查找，

③如果命中则结束，否则进入查询关键字所属范围的儿子结点；不断重复，直到所对应的节点指针为空

④关键字(查找的目标值)集合分布在整颗树中, 即目标值有可能是叶子节点或是非叶子节点

⑤关键字(查找的目标值)搜索有可能在非叶子结点结束。

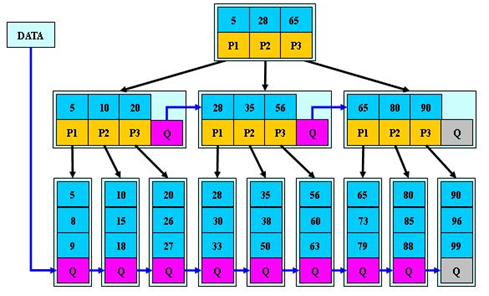
B+树

• 什么是B+树

B+树是B树的变体，也是一种多路搜索树。

• B+树的特点(其性能也等价于在关键字全集做一次二分查找)

①B+树的搜索与B树也基本相同，区别是B+树只有达到叶子结点才命中（B树可以在非叶子结点命中），

②所有关键字都出现在叶子结点的链表中（即数据只能在叶子节点【也叫稠密索引】），且链表中的

关键字(数据)恰好是有序的。

③不可能在非叶子结点命中

④非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层，

更适合文件索引系统

B*树

• 什么是B*树

B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针

• B*树的特点

①B* 树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3，而B+树的块的最低使用率为1/2。

②B*树分配新结点的概率比B+树要低，空间使用率更高

Q代表指向下一个节点

红黑树

实现红黑树的关键：变色和旋转(左旋或右旋)

• 红黑树的规则 == > 参考资料

①每个节点不是黑色就是红色(默认根节点为黑色，每一个插入的节点开始默认为红色)

②根节点为黑色

③红色节点的父节点和子节点不能为红色(或者说每个红色节点必须有两个黑色子节点)

④每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]

⑤从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点

• 平衡二叉树和红黑树的区别

①平衡二叉树的左右子树的高度差绝对值不超过1，但是红黑树在某些时刻可能会超过1，但还符合红黑树的五个条件

②二叉树只要不平衡就会进行旋转，而红黑树不符合规则时，有些情况只用改变颜色不用旋转，就能达到平衡。

---

图结构

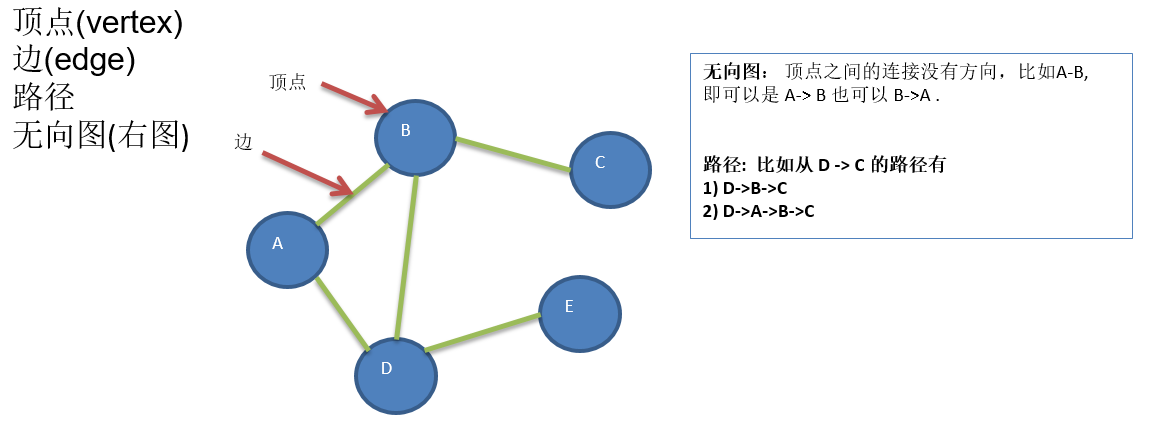
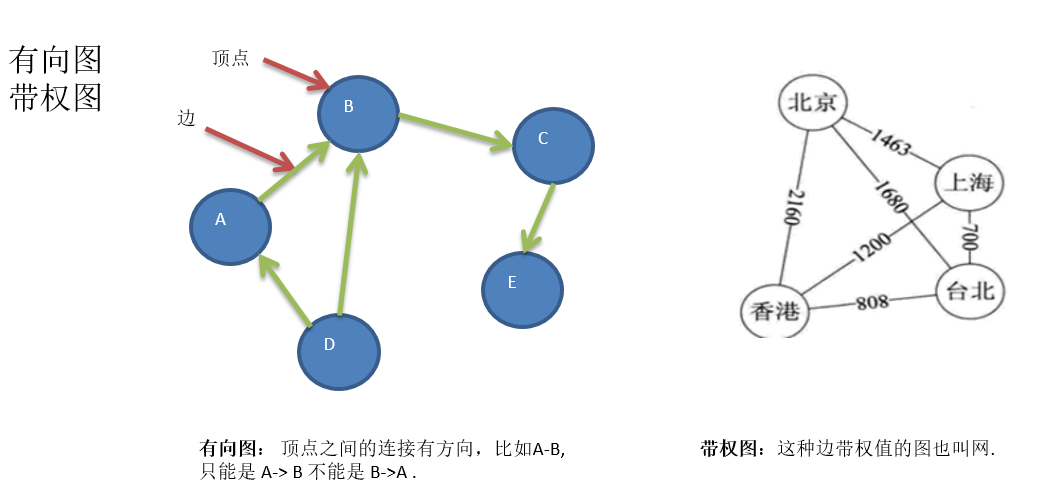
• 为什么需要图结构

因为在某种情况下需要表示多对多的关系，而线性表和树不能满足这个要求

• 什么是图以及图的基本概念

图是一种数据结构，其中结点可以具有零个或多个相邻元素。

两个结点之间的连接称为边。 结点也可以称为顶点。

• 图的表示方式

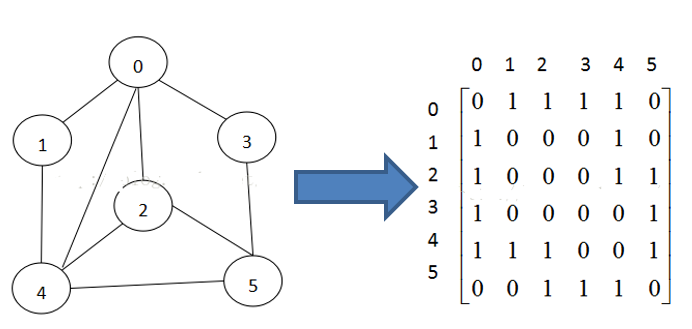
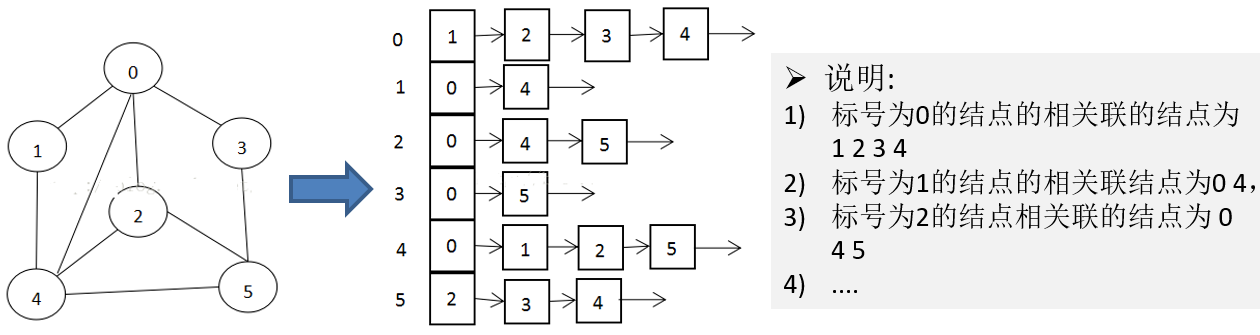
两种方式：二维数组表示（邻接矩阵）和 链表表示（邻接表）。

邻接矩阵：表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是的row和col表示的是1….n个点。

邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在,会造成空间的一定损失.

如何理解无向图的邻接矩阵是对称的？

如果记邻接矩阵为A，如果顶点i和顶点j，有一条边，那么矩阵元素值A(i，j)和A(j，i)是一样的，所以A是对称的。

邻接表：由数组+链表组成邻接表的实现，它只关心存在的边，不关心不存在的边，因此没有空间浪费

• 图的创建

public class GraphDemo {

    private static ArrayList<String> vertexList;//表示存储顶点的List
    private static int[][] edges;//表示无向图的邻接矩阵的二维数组
    private static int numOfEdge; //表示边的个数

    public static void main(String[] args) {
        GraphDemo graph = new GraphDemo(5);
        // graph.showGraphMatrix();
        String[] val = {"A","B","C","D","E"};
        for (String s : val) {
            graph.insertVertex(s);
        }

        graph.insertEdge(0,1,1);
        graph.insertEdge(0,2,1);
        graph.insertEdge(1,2,1);
        graph.insertEdge(1,3,1);
        graph.insertEdge(1,4,1);

        graph.showGraphMatrix();
    }

    public GraphDemo(int num){
        //初始化二维数组和list集合
        edges = new int[num][num];
        vertexList = new ArrayList<>(num);
    }

    /**
     * Description : 添加顶点
     * @date 2022/11/13
     * @param vertex 待添加的顶点
     **/
    public  void insertVertex(String vertex){
        vertexList.add(vertex);
    }

    /**
     * Description : 添加边
     * @date 2022/11/13
     * @param v1 表示当前第一个顶点在所对应的行数
     * @param v2 表示当前第二个顶点在所对应的列数
     * @param value 权值
     **/
    public void insertEdge(int v1,int v2,int value){
        //由于无向图的邻接矩阵是个对称矩阵，所以[v1][v2]或[v2][v1]的值都等于value；
        edges[v1][v2] = value;
        edges[v2][v1] = value;
        //边数+1
        numOfEdge++;
    }

---

算法

前置知识

时间频度：一个算法中的语句执行次数被称为语句频度或时间频度，记为**T(n)**。

​ 一个算法所花的时间与算法中语句的执行次数成正比例关系。

• 随着程序规模的增大时间频度通常可以忽略常数项、低次项、系数，进而影响算法的时间复杂度。

时间复杂度：一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，

​ 若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，

​ 则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n))，称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

• T(n)时间频度不同，但时间复杂度是有可能相同的

计算时间复杂度的方法：

①当时间频度为常数时，则时间复杂度为T(n)= O(1)

②当时间频度为多项式时，去除低阶项和高阶项的系数，但必须保留高阶项的次项

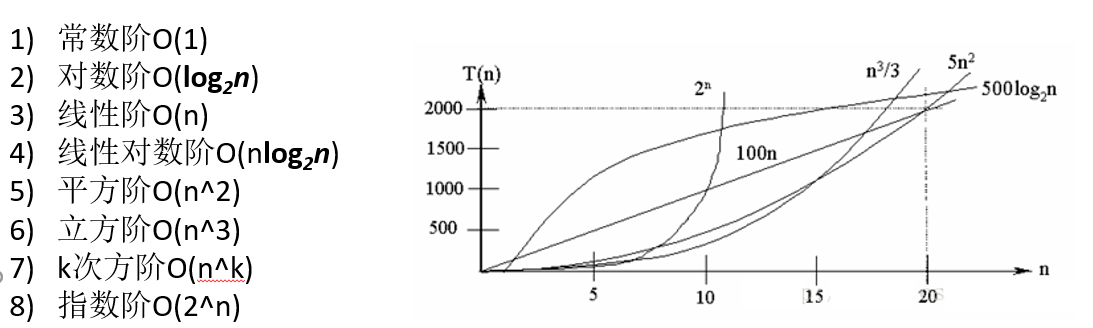
常见的时间复杂度

• 常数阶

• 对数阶

• 线性阶

• 线性对数阶

• 平方阶

• 立方阶

参考上面的O(n²) 去理解，O(n³)相当于三层n循环

• k次方阶

参考上面的O(n²) 去理解，O(n*k)相当于k层n循环

• 平均时间复杂度和最坏时间复杂度

①平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。

②最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。

因为这保证了算法的运行时间不会比最坏情况更长。

③平均时间复杂度和最坏时间复杂度是否一致，和算法有关

---

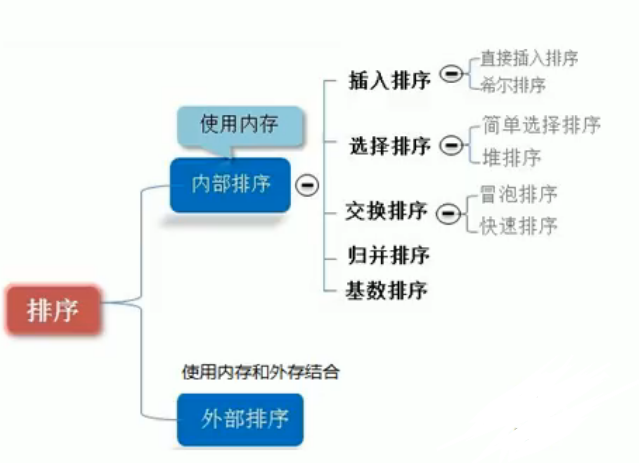
排序算法

排序：也称为排序算法，指将一组数据按照特定的顺序进行排列。

• 各排序算法比较

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；

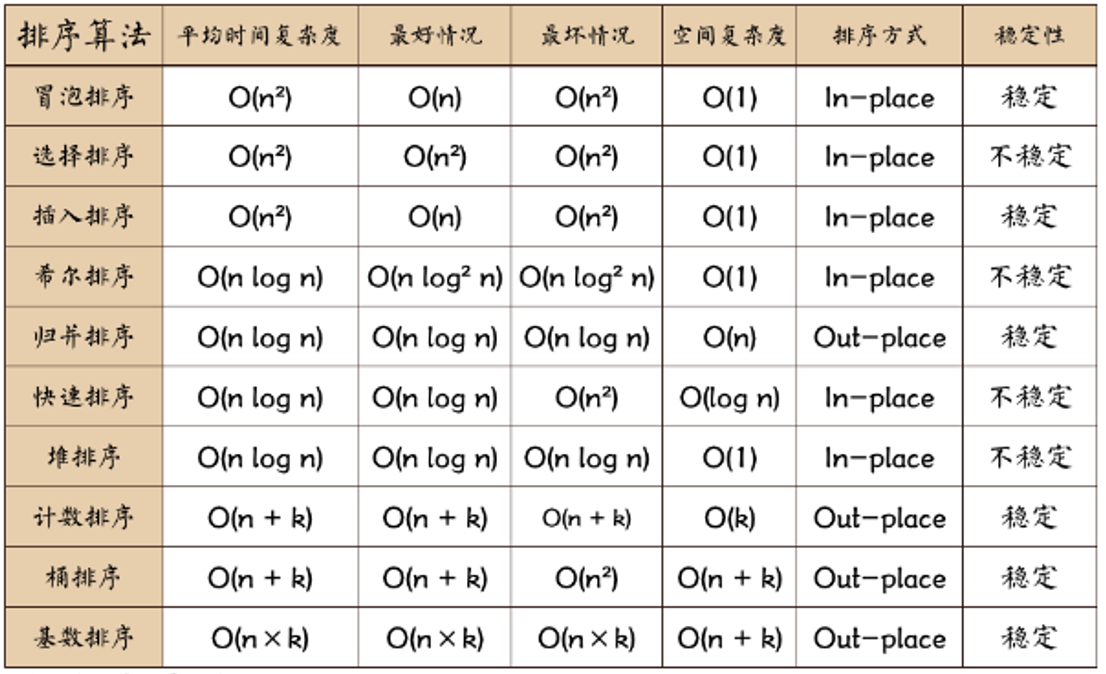
稳定性就是指排好序的相对顺序不变（比如有两个相同的数，前面那个排好后还是在前面）

不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；

内排序：所有排序操作都在内存中完成；

外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

时间复杂度：一个算法执行所耗费的时间。

空间复杂度：运行完一个程序所需内存的大小。

n: 数据规模

k: “桶”的个数

In-place: 不占用额外内存

Out-place: 占用额外内存

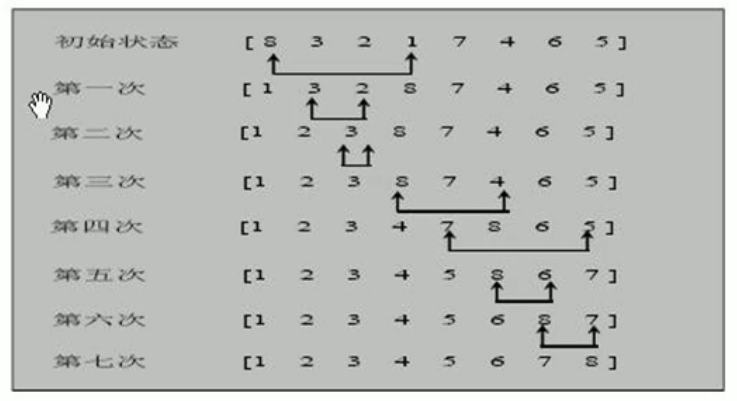
交换排序

冒泡排序

基本思想：通过对待排序序列从前往后，依次比较相邻元素的值，若发现逆序就立即交换，

​ 从而让数值大的元素，逐渐从前移向后面。

• 冒泡排序总共需要进n-1次排序次数

未优化版冒泡排序：

public static void main(String[] args) {
        int[] bubble = new int[]{3,9,-1,10,-2};
        //临时存储元素值
        int temp;
        /*
        只需要进行n-1次排序即可实现有序数组
        因为在第n次排序时，此时剩下的已经是最小的了，因此不需要再次比较
         */
        for (int i = 0;i<bubble.length-1;i++){
            /*
            每一次排序都是从第一个元素开始，因此下标为0
            例如，当i=0时，bubble.length-1-i 相当于 bubble.length-1
            而此时j最大只能取到 bubble.length-2，
            因此当     j = bubble.length-2
                      j+1 = bubble.length-2+1 ==> bubble.length-1
            保证了每次都能取到最后一个需要比较的元素。也正是因为如此
            在每轮i变化时。j的取值范围相应-i.从而保证每轮都可以避免每次索引都遍历到数组最后一个元素
             */
            for (int j = 0;j<bubble.length-1-i;j++){
                //比较相邻的两个元素
                if (bubble[j] > bubble[j+1]){
                    temp = bubble[j+1];
                    bubble[j+1] = bubble[j];
                    bubble[j] = temp;
                }
            }
        }
}

优化版冒泡排序(即当发现某次排序中没有进行任何交换提前结束排序)：

//优化版 即当发现某次排序中没有进行任何交换提前结束排序
public static void main(String[] args) {
    int[] bubble = new int[]{3,9,-1,10,20};
    //临时存储元素值
    int temp;
    //临时标识符，用于辨认是否需要结束排序
    boolean flag = false;
    for (int i = 0;i<bubble.length-1;i++){
        for (int j = 0;j<bubble.length-1-i;j++){
            //比较相邻的两个元素
            if (bubble[j] > bubble[j+1]){
                //表示执行过排序
                flag = true;
                temp = bubble[j+1];
                bubble[j+1] = bubble[j];
                bubble[j] = temp;
            }
        }
        if (!flag){ //表示没进行过交换，直接结束
            break;
        }else {
            //重置flag进行下一次交换
            flag = false;
        }
        System.out.println("当前是第" + (i+1) + "次排序");
    }
}

快速排序

快速排序是对冒泡排序的一种改进。

基本思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分

​ 所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归

​ 进行，以此达到整个数据变成有序序列

public static void soft(int[] array,int left,int right){
     //当left >= right代表需要排序的数组已经排序过了，不需要再次排序，直接结束
    //这一步很重要，这一步是递归结束的条件，没有这一步会陷入死循环中
    if (left >= right){
        return;
    }
    int l = left; //左边第一个元素，用于遍历比较
    int r = right;//右下标值
    int pivot = array[left]; //以第一个元素为基准值，用于比较
    /*
    这个循环是为了保证把左边所有比pivot大的值放到右边，
    把右边所有比pivot小的值放到左边，而当l == r也就说明所有的数都遍历比较过了
    */
    while (l != r){
       /* 找到右边比基准值小的下标就退出循环
          l < r是为了保证只遍历比较当前要求的数组范围，
          当array[r] >= pivot一直满足时，r会一直-1，会导致
          下面的array[l] = array[r]被错误赋值
        */
        while (l < r && array[r] >= pivot){
            r -= 1;
        }
        if(l < r){
            //上面循环是因为l<r不满足退出时，此时l和r是在同个位置
            array[l] = array[r];
        }
            
        //找到左边比基准值大的下标就退出循环，此处l<r和上面的原因一样
        while (l < r && array[l] <= pivot){
            l += 1;
        }
        if(l < r){
            array[r] = array[l];
        }
    }
    /* 出了上面的循环，代表此时l==r了，
       同时所有l左边的数都比pivot小，l右边的数都比pivot大，
       此时只需要把pivot的值赋于l或者r所在位置即可
    */
    array[l] = pivot;
    //因为无法保证在经过上面的排序后pivot左右两边的数已然有序，因此必须再对pivot左右两边进行递归快排
    //左边递归
    soft(array,left,l-1);
    //右边递归
    soft(array,l+1,right);
}

选择排序

选择排序：是从需要排序的数据中，按指定的规则选出某一元素，再根据规则交换位置达到排序

基本思想：从一个数组的首位到末位中选出最小值，与数组首位进行交换，不断重复这个过程，最终实现排序

• 注意：选择排序和冒泡排序存在一定相似性，但冒泡排序是比较相邻的两个元素，一旦逆序则立即交换，

  因此在每一轮有可能交换多次。而选择排序是通过不断遍历从开始位置到结束位置的元素，找到符合指定

  的数字，但不是找到一个就交换，而是找到最后一个位置，最终达到每一轮排序只交换一次的效果。

简单选择排序

• 这个排序会进行n-1轮，每一轮都会先确认最小值和其下标，待本轮结束后才交换

  与插入排序不同的是，它不涉及元素的后移，仅仅是确定位置后，本轮遍历结束后交换

//将某个数组从小到大进行排序
public static void sort(int[] array) {
        int minIndex = 0; //记录最小值的下标
        int min = 0; //假定第一个元素为最小的
        /*
        与冒泡排序相似，只需要执行array.length -1 轮排序即可确定数组的有序性
        例如总共7个数字，执行6轮后剩下最后的这个数就不需要再排序了
        ①确定总共需要进行几轮排序
        ②假定当前的数字为最小值，逐个遍历比较
        当下一个数字比当前数字大时，则将两个数值进行交换
         */
        for (int i = 0; i < array.length - 1; i++) {
            minIndex = i;
            min = array[i];
            for (int j = i+1; j < array.length; j++) {
                if (min > array[j]) {
                    minIndex = j;//重新设置最小值下标
                    min = array[j]; //重新设置最小
                }
            }
            //当minIndex == i时说明最小值下标没变化过，不需要做交换
            if (minIndex != i){
                //将数组最小值和数组首个元素进行交换
                array[minIndex] = array[i];
                array[i] = min;
            }
        }
    }

堆排序

堆排序：一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

• 堆是具有以下性质的完全二叉树

  每个结点的值都大于或等于其左右子结点的值，称为大顶堆(对左右节点值大小的关系不做要求)

  每个结点的值都小于或等于其左右子结点的值，称为小顶堆

• 大顶堆特点：arr[i] >= arr[2 * i+1] && arr[i] >= arr[2*i+2] // i 对应第几个节点，i从0开始编号

• 小顶堆：arr[i] <= arr[2 * i+1] && arr[i] <= arr[2*i+2] // i 对应第几个节点，i从0开始编号

• 一般升序选择将无序序列构建成大顶堆，降序将无序序列构建成小顶堆

基本思想：

1.先获取到最后一个非叶子节点(从上到下的角度)，

2.让当前非叶子节点所在的树成为局部大顶堆(至于此树的左右节点大小排序则没有要求)，

3.从下往上找到上一个非叶子节点，且从当前的非叶子节点从上到下进行调整为局部大顶堆

4.最后形成一个完整的大堆顶

5.再交换数组的第一个元素(堆顶)和最后一个元素(堆末)，并重新构建堆结构(从新的堆顶元素开始从上往下调整)

6.最后再反复执行第5步，直至成为了一个小堆顶，此时序列已然有序

/**
     * Description : 堆排序的实现
     * @date 2022/10/18
     * @param array 传入的数组
     **/
public static void sort(int[] array){
    //1.将无序序列构建成一个完整的大顶堆
    for (int i = array.length/2-1; i >= 0 ; i--) {
        adjustHead(array,i,array.length);
    }

    //交换元素并重新构建大堆顶
    int temp = 0;
    for (int i = array.length-1; i >= 0 ; i--) {
        //交换数组的第一个元素(堆顶)和最后一个元素(堆末)
        temp = array[i];
        array[i] = array[0];
        array[0] = temp;
        /* 因为每次堆顶和堆末的元素交换都会破环大顶堆的结构，且每次构建必须
               排除掉已经放到堆末的那个元素，从当前的栈顶重新构建堆结构
             */
        adjustHead(array,0, i);
    }
}

/**
     * Description : 构建一个完整的大顶堆
     * @param array 传入的数组
     * @param nodeIndex 当前最后一个非叶子节点
     * @param length 数组长度
     **/
public static void adjustHead(int[] array,int nodeIndex,int length){
    //保存当前父节点的值
    int temp = array[nodeIndex];
    /* 这里解释一下为什么需要i = i*2+1，和在if后面添加else的逻辑
        看起来完全不需要是吧，因为首先传入的是最后一个非叶子节点所以会让
        这些步骤看起来像是多余的，但是一旦执行到最后一个非叶子节点的上一个
        非叶子节点就非常需要，因为无法确认当前的非叶子节点下的节点是否都满足
        大顶堆的要求，即当前节点比其下的所有左右节点都要大，因此必须去判断它
        下面所有左右子节点是否都小于(而左节点是否小于右节点也做了判断)，
        说白就是为被替换下来的节点再次找到合适的位置
         */
    for (int i = (nodeIndex*2+1); i < length; i = i*2+1) {
        /*判断左子节点是否小于右子节点，经过这步，无论是左节点大于还是小于右节点，
            此时i指针都是指向两个节点中的最大值那个
            */
        if (i+1 < length && array[i] < array[i+1]){
            i++;
        }
        //判断子节点最大值是否大于父节点
        if (array[i] > temp){
            //将父节点的值赋为子节点最大值
            array[nodeIndex] = array[i];
            //将i指针指向子节点中最大值所在位置
            nodeIndex = i;
        }else{
            break;
        }
        //将子节点中最大值修改为原先的父节点值，完成两数交换
        array[nodeIndex] = temp;
    } 
}

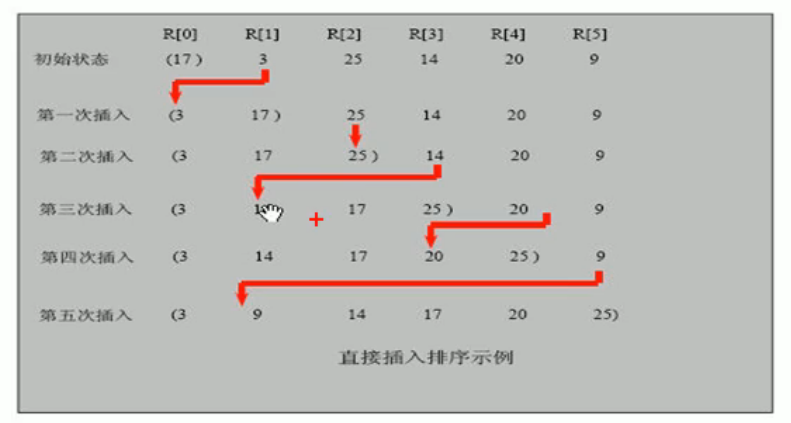
插入排序

直接插入排序

直接插入排序：将需要排序的元素以插入的方式寻找该元素的适当位置，达到排序的目的

基本思想：把n个待排序的元素看成一个有序表和一个无序表，在最开始时有序表中只有一个元素，无序表

有n-1个元素，在每次排序都会从无序表中取出第一个元素，将它的排序码与有序表元素的排序码进行比较，

将其拆入到有序表中的适当位置，从而形成新的有序表

• 这个排序是将大于插入值的元素后移，并遍历比较查找到插入位置后，本轮遍历结束后插入

/*
基本思路：
①将第一个需要插入的元素数值保存起来，用一个临时变量存储待插入元素的下标值
②再将其与前一个元素进行比较
③判断是否需要进行交换并找到插入位置
④将需要插入的元素值插入到指定位置
*/
public static void soft(int[] array){
    for (int i=0;i< array.length-1;i++){
        int insertVal = array[i+1];
        int insertIndex = i;
        /*
        insertIndex >= 0 保证了数组角标不会越界
        insertVal < array[insertIndex] 保证了插入元素数值一定比前一个元素小
         */
        while (insertIndex >= 0 && insertVal < array[insertIndex]){
            //将大于插入位置元素值的元素后移
            array[insertIndex + 1] = array[insertIndex];
            //考虑到插入位置前有可能有多个元素，因此需要--多次判断
            insertIndex--;
        }
        /* 当退出循环代表已经找到需要插入的位置了
         insertIndex + 1是考虑到两种情况：
          1.最小值在最右边，需要放到第一个元素的位置，而当退出循环找到插入位置时，
            此时insertIndex = -1，因此必须+1才能保证元素的正常插入到第一位
          2.其插入的位置就这原来的位置上的情况，例如[34，35]的情况，期望插入位置为0，
            实际插入位置为1，35又大于34，因此不可能能进入循环中，也必须+1保证元素的正常插入
         */
        array[insertIndex + 1] = insertVal;
        }
    }
}

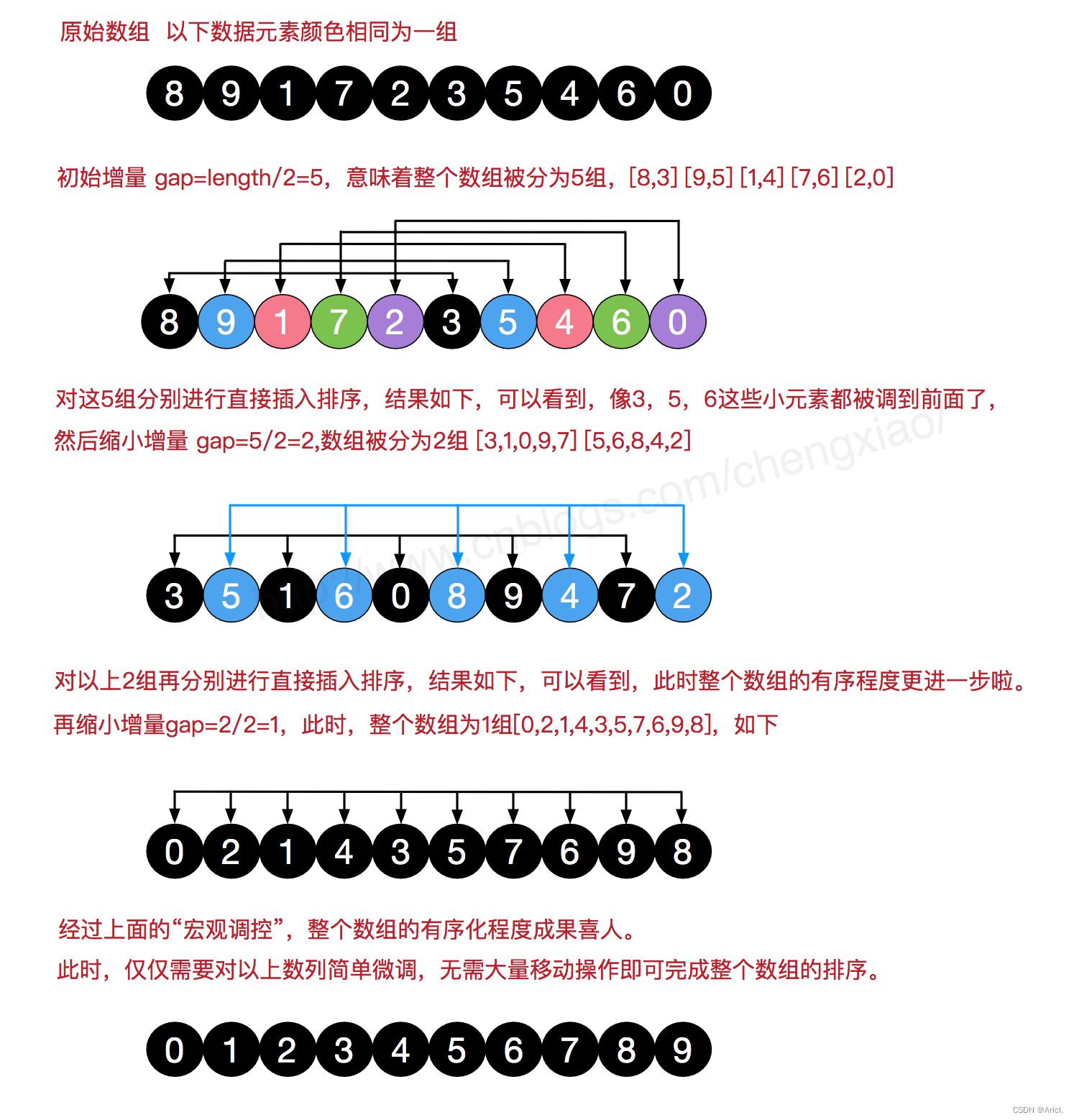
希尔排序

希尔排序：在直接插入排序的基础上经过改进的更高效排序，也被称为缩小增量排序

基本思想：把记录按照下标的一定增量分组，对每组使用直接插入排序；随着增量逐渐减少，

每组包含的关键词越来越多，当增量减至1时，整个文件刚好被分成一组，再次直接插入排序便结束排序

• 因为当一个数组的大部分元素是从大到小排列，如果按照从小到大排序，效率会降低（需要很多次交换）

  而在这种情况用希尔排序就能提升排序效率。

• 移位法是直接从gap增量此时的值对应下标的数开始向前比较，并判断是否需要交换

public class ShellSortTest {
    /*
    希尔排序移位法实现，从第gap个元素开始遍历，并不断比较在gap元素前的同组元素
     */
    public static void softShell(int[] array) { //所需时间为1s
        int insertIndex = 0;
        int insertVal = 0;
        for (int gap = array.length/2; gap > 0 ; gap /= 2) {
            //直接从第gap个元素开始，对其所在的组进行直接插入排序，相当于假设当前i所在的位置就是插入的位置
            for (int i = gap; i < array.length; i++) {
                insertIndex = i;
                insertVal = array[insertIndex];
                if (insertVal < array[insertIndex - gap]){
                    //insertIndex - gap >= 0是为了判断前面是否还有数需要比较，
                    //不成立则说明上一次比较后的insertIndex就是需要插入的位置
                    while (insertIndex - gap >= 0 && insertVal < array[insertIndex - gap]){
                        array[insertIndex] = array[insertIndex - gap];//将较大的元素后移
                        insertIndex -= gap;//重置元素插入位置
                    }
                    array[insertIndex] = insertVal;
                }
            }
        }
    }

    /*
    希尔排序交换式实现 所需时间5s 正序遍历比较
    实际上这种方法就是分组加上每个元素循环遍历比较，效率较低
     */
    public static void soft(int[] array) {
        int insertVal = 0;
        int gap = array.length /2;
        while (gap != 0) {//gap是步长(增量)，当gap=0时，数组已经是有序了
            for (int i = 0; i < array.length; i++) {
                //下面的循环是为了分组后找到需要比较的组和遍历比较组内的所有元素，
                for (int j = i + gap; j < array.length; j += gap) {
                    //保存当前的元素值
                    insertVal = array[j];
                    //进行比较，当此时元素大于加上步长的元素则进行交换
                    //相当于发现一个就立即交换
                    if (array[i] > array[j]) {
                        array[j] = array[i];
                        array[i] = insertVal;
                    }
                }
            }
            gap = gap / 2; //减少增量
        }
    }
}

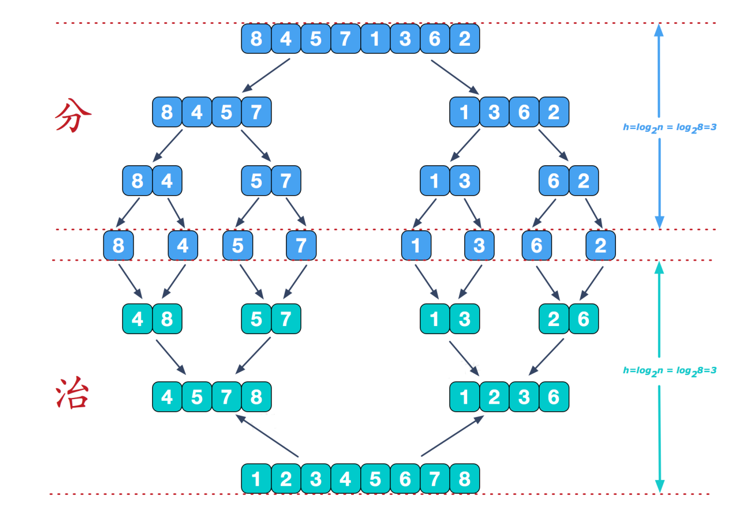
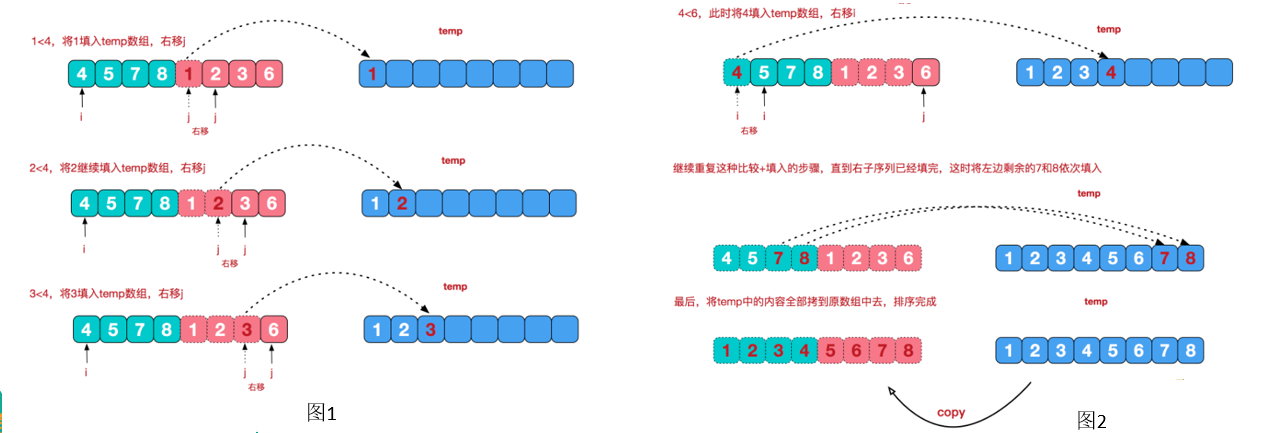
归并排序

归并排序(MERGE-SORT)：利用归并的思想实现的排序，该算法采用分治(divide-and-conquer)策略

• 什么是分治策略(可以理解为分而治之)

分治法将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案”修补”在一起

public class MergeSortTest {
    /**
     * Description : 递归拆分排序数组+合并成有序数组
     * 分治法中所谓的分就是将一个数组不断左右递归拆分，
     * 但仅仅是字面意思上的拆分，并不是真正将一个数组拆分成多个数组，
     * 只是通过多个下标指针限定每次遍历的范围。
     * 而每次的递归都是左右递归拆分，直至不能再拆分后就进行合并。
     * 这里很复杂，因为递归是压栈操作，每次都先执行完栈顶方法才会执行下一层，
     * 但是会在某一层中又会发生递归分解，重复拆分合并的操作。
     * 直至栈内所有方法执行完毕
     * @param array 传入的数组
     * @param left 数组左边的下标
     * @param right 数组右边的下标
     * @param temp 临时存储交换值所用数组
     **/
    public static void mergeSoft(int[] array,int left,int right,int[] temp){
        //该条件成立则传入的数组不需要递归分解
        if (left >= right){
            return;
        }
        int mid = (left + right) / 2;
        //向左递归分解
        mergeSoft(array,left,mid,temp);
        //向右递归分解
        mergeSoft(array,mid+1,right,temp);
        //合并
        merge(array,left,right,mid,temp);
    }

    /**
     * Description : 合并数组
     * @date 2022/10/4
     * @param array 排序的原始数组
     * @param left 左边有序序列的初始下标
     * @param right 右边下标
     * @param mid 中间下标
     * @param temp 临时存储交换值所用数组
     **/
    public static void merge(int[] array,int left,int right,int mid,int[] temp){
        // System.out.println("原数组:" + Arrays.toString(array));
        int l = left; //左边数组的下标
        int m = mid + 1; //右边第一个数组的下标
        int t = 0;//当前temp数组所在位置下标

        /* 先将左右两边有序的数据按照规则填充到temp数组中
           直至左右两边的有序序列，有一边处理完毕
           l <= mid 确保了只遍历由原数组分出的左边数组，
           m <= right 确保了只遍历由原数组分出的右边数组，
           实际上这些都是在同一个数组中，同个mid和right限制遍历范围
         */
        while (l <= mid && m <= right){
            //满足if则代表左边的比右边的数小
            //需要将当前左边的数放到temp这个临时数组中
            if (array[l] <= array[m]){
                temp[t] = array[l];
                t++;
                l++;
            }else {
                temp[t] = array[m];
                t++;
                m++;
            }
        }

        /*
        将有剩余数据的有序序列中的数据依次添加到temp数组中
        当由于m不满足条件退出上面while循环时，此时m是比数组长度还是大于1的
        因此m-1 == right是用来判断此时右边数组是否已完全遍历了
         */
        if (m-1 == right){
            for (int i = l; i <= mid ; i++) {
                temp[t] = array[i];
                t++;
                l++;
            }
        }else{
            for (int i = m; i <= right ; i++) {
                temp[t] = array[i];
                t++;
                m++;
            }
        }

        /*
        将temp数组的数据复制到原始的数组中
        insertIndex将插入位置设为分解array数组后传入的第一个元素所在的位置
        t表示临时数组temp中有多少个元素
         */
        int insertIndex = left;
        for (int i = 0; i < t; i++) {
            array[insertIndex] = temp[i];
            //因为不知道传入的分解数组有多少个元素，
            // 因此需要+1，才能保证temp的元素正确插入array数组中
            insertIndex++; 
        }
    }
}

基数排序

基数排序是1887年赫尔曼·何乐礼发明的，属于“分配式排序”(distribution sort)，又称“桶子法”(bucket sort)

基数排序(radix sort)：它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，达到排序的作用。

基本思想：将整数按位数切割成不同的数字，然后按每个位数分别比较。

​ 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

• 基数排序(Radix Sort)是桶排序的扩展，它是使用空间换时间的算法，但是有负数则不建议使用此排序

  因为如果数组中有负数，取余后num为负数，则在赋值时出现角标越界。

基数排序图解

public static void radixSoft(int[] array){
        //创建一个二维数组表示10个桶
        int[][] bucket = new int[10][array.length];

        /* 创建一个一维数组，该数组下标对应的值表示10个桶各自当前下标所在的位置
           该数组的值不需要重置，仅仅是临时记录下标位置，会被反复覆盖
         */
        int[] bucketIndex = new int[10];

        //先找到最大的数
        int max = 0;
        for (int i = 0; i < array.length; i++) {
            if (max < array[i]){
                max = array[i];
            }
        }

        int chuNum = 1; //定义每轮需要先除的数字
        int loop = String.valueOf(max).length(); //总共循环比较次数
        int loopNum = 0; //初始化循环次数
        while (loopNum < loop) {
            //遍历比较
            for (int i = 0; i < array.length; i++) {
                int num = array[i] / chuNum % 10 ; //代表应该放在那个桶中
                /* 因为bucketIndex的每个下标都代表对应的桶元素的下标位置
                   因此取余后两个数的num相同，即都会指向bucketIndex数组中同一个下标
                   bucketIndex[num]是维护了每一个桶内元素的索引
                   bucketIndex[num]++才能保证桶内前一个元素不会被当前的元素覆盖
                   PS:假设数组中有负数，取余后num为负数，则下方这一步会出现角标越界
                 */
                bucket[num][bucketIndex[num]] = array[i];
                bucketIndex[num]++;
            }

            int index = 0;
            for (int i = 0; i < bucket.length; i++) {
                for (int j = 0; j < bucket[i].length; j++) {
                    if (bucket[i][j] != 0){ //不为0代表有数据
                        array[index] = bucket[i][j]; //将当前位置数赋到原数组位置
                        index++;
                        /* 必须重置当前位置数为0，为下一轮排序做准备，
                       例如下一轮这个位置没有数字，而本轮没重置导致此处位置不为0，
                       本不该进入此结构却进来了，就会破坏原数组的排序数。
                         */
                        bucket[i][j] = 0;
                    }
                }
            }
            chuNum *= 10; //为下一轮取模前除数做准备
            loopNum++;
        }
    }

---

查找算法

线性查找

线性查找也称为顺序查找

public static int search(int[] array,int num){
        for (int i = 0; i < array.length; i++) {
            if (num == array[i]){
                return i; //代表已找到
            }
        }
        return -1; //代表未找到
    }

二分查找

二分查找也称折半查找，二分查找的前提要求数组必须是有序的

public static int search(int[] array,int num,int left,int right) {
    //先找中间数
    int mid = (left + right) / 2;
    /*
        当遍历到最右边时，left是等于right+1的
        当遍历到最左边时，right是等于-1的，
        因此left > right能保证遍历的范围一定在数组的下标范围内
     */
    if (left > right){
        return -1;
    }
    if (array[mid] == num) { //说明要找的数刚刚好是中间数
        return mid;
    } else if (array[mid] > num) { //说明要找的数还在mid左边
        right = mid-1;
        return search(array, num, left, right); //把查找到的下标一层层返回
    } else if (array[mid] < num) { //说明要找的数还在mid右边
        left = mid+1;
        return search(array, num, left, right); //把查找到的下标一层层返回
    }
    return -1;
}

插值查找

插值查找：插值查找算法类似于二分查找，但不同的是插值查找每次是从自适应mid处开始查找

• 插值查找的前提也要求数组必须是有序的

基本思想：将折半查找中的求mid 索引的公式 , low 表示左边索引left, high表示右边索引right.

​ key 就是要找的目标数

公式：int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low])

• 插值查找注意事项：

  ①对于数据量较大，关键字(数组元素的值)分布比较均匀的查找表来说，采用插值查找, 速度较快.

  ②关键字分布不均匀(数值跳跃性很大)的情况下，该方法不一定比二分查找效率较高

public static int search(int[] array,int left,int right,int num){
    //num < array[left] || num > array[right]这两个条件很有必要，
    //否则当传入的num值远远大于数组最大值时，会出现角标越界异常
    if (left > right || num < array[left] || num > array[right]){
        return -1;
    }
    int mid = left + (right - left) * (num - array[left]) / (array[right] - array[left]);
    int numValue = array[mid];

    if (numValue == num){
        return mid;
    }else if (numValue > num){ //说明要找的数还在mid的左边
        right = mid - 1;
        return search(array,left,right,num);
    }else if (numValue < num){ //说明要找的数还在mid右边
        left = mid + 1;
        return search(array,left,right,num);
    }
    return -1;
}

斐波那契查找

斐波那契查找也称为黄金分割法

• 黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽，因此称为黄金分割，也称为中外比

• 斐波那契数列即两个相邻数的比例，无限接近黄金分割值0.618

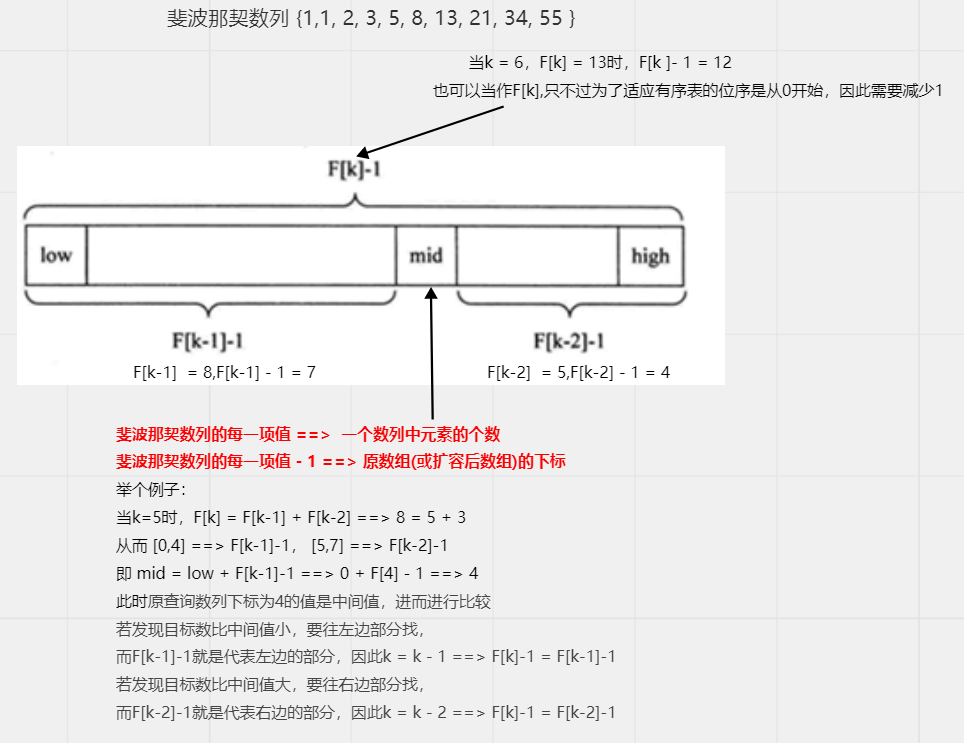
基本思想：通过改变了中间结点（mid）的位置，但mid不再是中间或插值得到，而是位于黄金分割点附近，

​ 即mid=low+F(k-1)-1（F代表斐波那契数列），通过斐波那契数组来辅助确定mid的值

• 由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质，可以得到（F[k]-1）=（F[k-1]-1）+（F[k-2]-1）+1,

  该式说明：只要顺序表的长度为F[k]-1，则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,

  从而中间位置为mid=low+F(k-1)-1

• 类似的，每一子段也可以用相同的方式分割

• 但顺序表长度n不一定刚好等于F[k]-1，所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得

  F[k]-1恰好大于或等于n即可，由以下代码得到,顺序表长度增加后，新增的位置（从n+1到F[k]-1位置）,

  都赋为n位置的值即可。

public class FibonacciSearch {
    public static int maxSize = 20;
    /**
     * Description : 查找传入的数组的指定数
     * @date 2022/10/11
     * @param array 传入的原数组
     * @param num 目标数
     **/
    public static int search(int[] array,int num){
        int low = 0;
        int high = array.length-1;
        int k = 0;//斐波那契分割数值的下标
        int mid = 0;//用于判断的mid值
        int[] f = fib(); //斐波那契数列

        //先判断当k等于何数时数组元素个数大于或等于斐波那契数组的某个值
        while(high >f[k]-1){
            k++;
        }

        int[] copy = new int[0];
        /*
        当有序表的元素个数不是斐波那契数列中的某个数字时，须要把有序表的元素个数长度补齐，
        让它成为斐波那契数列中的一个数值，固然把原有序表截断确定是不可能的，否则还怎么查找。
        而后图中标识每次取斐波那契数列中的某个值时(F[k])，都会进行-1操做，这是由于有序表数组位序从0开始的，
        纯粹是为了迎合位序从0开始。
         */
        if (high <= f[k]-1){
            copy = Arrays.copyOf(array, f[k] - 1);
            int highVal = array[high];
            int tempHigh = high;
            int index = ++tempHigh;
            while (index < copy.length){
                copy[index++] = highVal;
            }
        }
        //当low大于high时代表以及遍历过数组最后一位了
        while (low <= high) {
            //再求出mid的值
            mid = low + f[k - 1] - 1;

            //用mid的下标对应的值和目标数进行比较
            if (copy[mid] == num) {
                /* 因为有可能原数组经过扩容，mid有可能找到扩容后下标去
                因此必须判断要找的值是mid下标对应的值时，mid是否已经超过原数组的high
                 */
                if (mid <= high){ //表示当前mid值尚未超过原数组high
                    return mid;
                }else { //表示当前mid值已超过原数组high
                    return high;
                }
            } else if (copy[mid] > num) { //说明要找的数还在mid左边
                high = mid - 1;
                /*
                k--的原因：
                1.全部元素 = 前面元素 + 后面元素
                2.f[k] = f[k-1] + f[k-2]
                因为前面有f[k-1]个元素所以，可以继续拆分 f[k-1] = f[k-2] + f[k-3]
                即在f[k-1]的前面继续查找k--
                即下次循环 mid = f[k-1-1] - 1
                */
                k--;
            } else if (copy[mid] < num) { //说明要找的数还在mid右边
                low = mid + 1;
                /*
                k-=2的原因：
                1.全部元素 = 前面元素 + 后面元素
                2.f[k] = f[k-1] + f[k-2]
                因为后面有f[k-2]个元素所以，可以继续拆分 f[k-1] = f[k-3] + f[k-4]
                即在f[k-2]的后面继续查找k-=2
                即下次循环 mid = f[k-1-2] - 1
                */
                k-=2;;
            }
        }
        return -1;
    }
    //mid = low + F[k-1]-1 需要使用斐波那契数列，因此先生成一个这种数列
    public static int[] fib(){
        int[] temp = new int[maxSize];
        temp[0] = 1;
        temp[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            temp[i] = temp[i-1] + temp[i -2];
        }
        return temp;
    }
}

---

赫夫曼编码

• 概念

赫夫曼编码也称为哈夫曼编码(Huffman Coding)或霍夫曼编码，是一种编码方法, 属于一种程序算法

赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。

赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间

赫夫曼码是可变字长编码(VLC)的一种，称之为最佳编码

前缀编码：字符的编码都不能是其他字符编码的前缀， 即不能匹配到重复的编码

• 实现思路(可变字长编码)

1.根据给定的字符串统计字符串中各个字符出现的次数

2.根据字符出现的次数作为节点权值创建一个赫夫曼树

3.给各个字符设置编码(前缀编码)，将这个赫夫曼树通往左边的编码设置为0，通往右边的编码设置为1

4.根据上述的字符编码将给定的字符串转换赫夫曼编码(这里实现了无损压缩)

5.经过上述操作，数据文件得到了压缩，给定字符串的长度压缩减少了60%左右。

PS：①在这个过程不会出现二义性(即某个字符编码是其他字符编码的前缀)，因为每个节点都是叶子节点，

其访问的路径都是唯一的，不会重复 ②这个赫夫曼树根据排序方法不同也可能不太一样，对应的赫夫曼

编码也不完全一样，但是wpl是一样的，都是最小的, 比如: 如果我们让每次生成的新的二叉树总是排在权值

相同的二叉树的最后一个和让每次生成的新的二叉树排在权值相同的二叉树的最前面，会导致生成的两个赫

夫曼树的树排列图看起来不一样。

暂时跳过，有空再补

---

图的遍历

深度优先(DFS)

• 深度优先(depth first search)

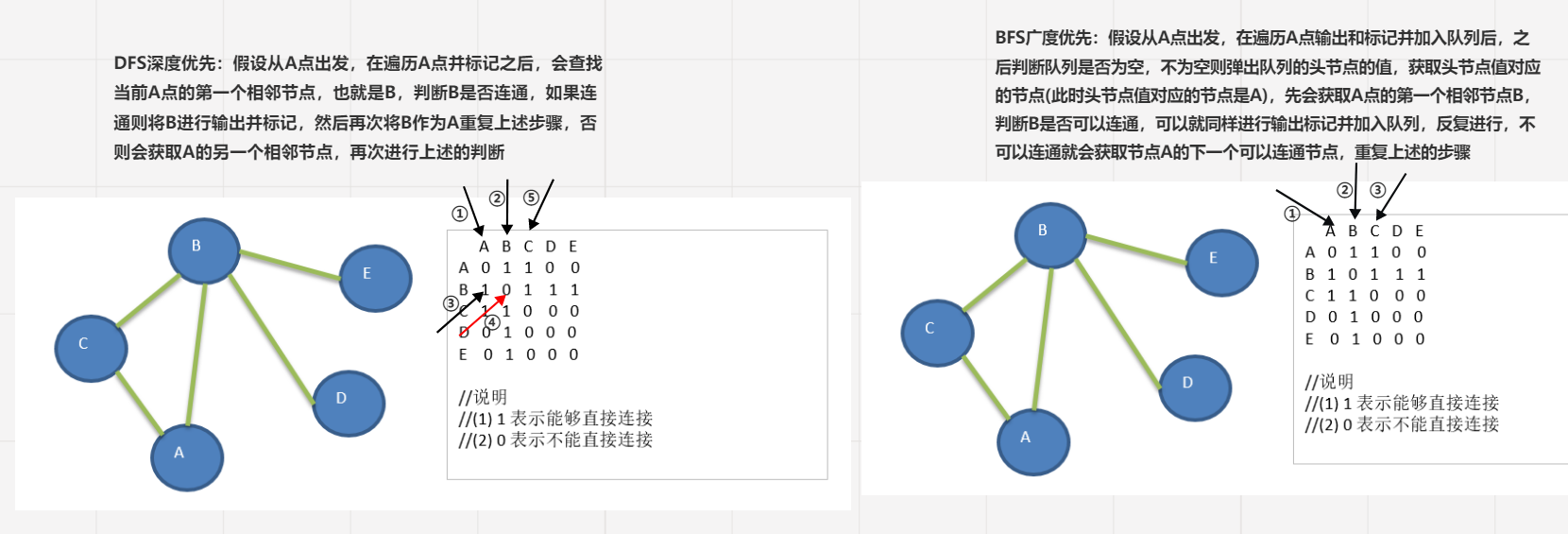
从初始结点出发，首先遍历第一个邻接结点，然后再以被遍历的邻接结点作为初始结点，

访问它的第一个邻接结点， 若发现第一个邻接结点不通，再寻求初始节点的其他相邻结点

若皆不通，则回退到刚刚访问过的节点寻找它的相邻节点，不断循环，直至遍历结束。

换句话来说就是 一条路走到黑为止

• 算法实现步骤

①遍历初始节点 标记为已遍历

②得到初始节点的第一个相邻节点

判断第一个相邻节点的情况

Ⅰ判断是否存在(不存在，返回到刚刚访问过的节点寻找它的相邻节点)

Ⅱ判断是否已被遍历(已遍历，返回到刚刚访问过的节点寻找它的相邻节点)

③以当前的相邻节点作为初始节点重复以上步骤

/**
* Description : 找到当前顶点的第一个相邻顶点的下标
* @param index 当前顶点索引
**/
public int getFirstNearVertex(int index){
    for (int i = 0; i < vertexList.size(); i++) {
        if (edges[index][i] != 0){
            return i;
        }
    }
    return -1;
}

/**
* Description : 找到当前顶点的下一个相邻顶点的下标
* @param indexRow 当前顶点索引所在行
* @param indexColumn 当前顶点索引所在列
**/
public int getNextNearVertex(int indexRow,int indexColumn){
    for (int i = indexColumn+1; i < vertexList.size(); i++) {
        if (edges[indexRow][i] != 0){
            return i;
        }
    }
    return -1;
}

/**
* Description : 深度优先算法
* @param index 传入要遍历的顶点索引
**/
public void dfs(int index){
    //获取目标顶点
    String v = getVertexOfValue(index);
    //输出并将index对应的顶点标记为已遍历
    System.out.println(v);
    beReadVertex[index] = true;

    //查找第一个相邻顶点
    int w = getFirstNearVertex(index);
    //判断w存在情况
    //这里的while相当于遍历二维数组中某一行的所有列。也就是判断某个顶点和其他顶点的关系
    while (w != -1){ //w != -1表示存在
        //判断是否已被遍历，取反为true表示未被遍历，再次执行dfs深度算法
        if (!beReadVertex[w]){
            dfs(w);
        }
        //没有进入上面的if函数表示已被遍历，需要找到当前顶点的其他相邻顶点
        w = getNextNearVertex(index,w);
    }
}

/**
* Description : 图的顶点不一定是相连的，比如非连通图，某个节点和其他节点都不相通，
* 没有这个方法会无法遍历到这个独立的节点，因此这个重载的方法非常有必要。
* 其实就是连通图和非连通的区别所导致的，这里跟回溯没有关系，
* 只是为了遍历在上面dfs深度算法中没有被遍历到的不连通的节点
**/
public void dfs(){
    for (int i = 0; i < vertexList.size(); i++) {
        //找到未被遍历的单独节点进行输出
        if (!beReadVertex[i]){
            dfs(i);
        }
    }
}

广度优先(BFS)

• 广度优先(Broad First Search)

类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，

以便按这个顺序来访问这些结点的邻接结点。换句话来说广度优先就是先将某一行的能够

访问的节点先全部遍历，有点类似树的层序遍历

• 算法实现步骤

①先创建队列

②输出下标对应节点并标记为已遍历同时将当前节点入队列

③判断队列是否为空

不为空弹出当前队列的头节点并找到对应下标的节点

④找到当前队列头节点下标值的相邻节点

⑤判断相邻节点是否存在

Ⅰ如果存在再判断是否已被遍历

Ⅱ尚未遍历则输出当前节点并标记为已遍历，同时加入队列中

Ⅲ再次寻找当前头节点下标值对应节点其他能够连通但尚未遍历的节点

public void bfs(int index){
    //创建存储顶点访问顺序的队列
    LinkedList<Integer> queue = new LinkedList<>();

    System.out.print(getVertexOfValue(index) + "=>");
    beReadVertex[index] = true;

    //将当前节点索引加入队列
    queue.add(index);
    int u; //当前队列当前头节点所对应的下标
    int w; //当前顶点的邻接顶点

    //判断队列此时是否为空
    while (!queue.isEmpty()){
        //表示此时所有的节点都被遍历过了，没必要再次进行剩下的尝试
        if (beReadVertex[beReadVertex.length-1]){
            return;
        }
        //输出并标记为已遍历
        u = queue.poll();
        //获得当前头节点对应下标的邻接节点
        w = getFirstNearVertex(u);
        //这个wilie的判断条件其实就是在判断w是否存在
        while (w != -1){ //代表找到
            if (!beReadVertex[w]){ //取反为true表示未被遍历
                //输出并标记为已遍历、加入队列
                System.out.print(getVertexOfValue(w) + "=>");
                beReadVertex[w] = true;
                queue.add(w);
            }
            //查找当前结点u的继w邻接结点后的下一个邻接结点w,这里体现出了广度优先
            w = getNextNearVertex(u,w);
        }
    }
}
/**
     * Description : 与上面的深度优先算法的重载方法dfs的原因一样，都是为了遍历非连通图的中的孤立顶点
     * @date 2022/11/15
     **/
public void bfs(){
    for (int i = 0; i < vertexList.size(); i++) {
        if (!beReadVertex[i]){
            bfs(i);
        }
    }
}

DFS与BFS的区别

①DFS深度优先更倾向于纵向遍历，而BFS更倾向于横向遍历

②DFS一般使用栈和回溯来实现，BFS一般使用队列来实现

③DFS占用的空间较小，BFS占用的空间较大

---

常用算法

二分查找(非递归)

/**
* Description : 二分查找(非递归)
* 关键是不断判断middle的值是否为目标值
* 因此middle的值必须放在循环中，根据start和end的变化而变化
* @param array 待查找的数组
* @param num 目标值
**/
public static int binarySearch(int[] array,int num){
    //先获取数组的头索引和尾索引值
    int start = 0;
    int end = array.length-1;
    while (start <= end){
        int middle = (start+end)/2;
        //代表刚刚好是中间数
        if (num == array[middle]) {
            return middle;
        }else if (num > array[middle]){ //表示要找的数还在中间数的右边
            start = middle + 1;
        } else if (num < array[middle]) { //表示要找的数还在中间数的左边
            end = middle - 1;
        }
    }
    return -1;
}

分治算法

分治算法的基本思想：将某个具有一定规模的大问题通过一定的方式分解成多个小问题，通过解决多个

小问题从而找到解决这个大问题的方案。

/**
     * Description : 将盘移动到C塔(递归+分治解决)
     * @date 2022/11/19
     * @param num 当前盘的数量
     * @param a a塔 起始地点
     * @param b b塔 中转使用
     * @param c c塔 目标地点
     **/
public static void hanoiTower(int num,char a,char b,char c){
    //表示只有一个盘
    if(num == 1){
        System.out.println("第1个盘，从 " + a + " => " + c );
    }else { //表示有两个盘以上
        // 如果有 n >= 2 情况，总是可以看做是两个盘 1.最下面的盘 2. 上面的盘
        // 先把 最上面的盘 A->B，移动过程中会使用到C塔
        hanoiTower(num - 1,a,c,b);
        // 把最下面的盘 A->C
        System.out.println("第" + num + "个盘，从 " + a + " => " + c);
        // 把B塔的所有盘 从 B->C，移动过程中会使用到A塔
        hanoiTower(num - 1,b,a,c);
    }
}

动态规划

• 什么是动态规划(Dynamic Programming)算法

这个算法的核心思想就是将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法

• 与分治算法的区别

与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。

( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )

• 01背包问题(动态规划算法实现)

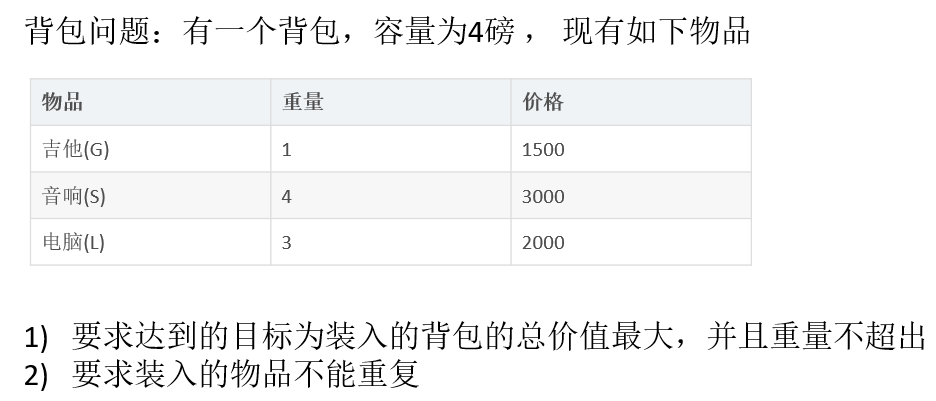
背包问题是指给一个定容量的背包及若干个一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。

其中又分01背包(每种物品最多放一个)和完全背包(完全背包指的是：每种物品可以无限件放入)

而无限背包可以转化为01背包。

实现思路：

public static void main(String[] args) {
    int[] weight = {1,4,3};//维护物物品重量的数组
    int[] value = {1500,3000,2000};//维护物物品价值的数组
    int m = 4;//背包容量
    int n = value.length;//物品的个数
    int[][] dp = new int[n+1][m+1];//表示在前i个物品中能够装入容量为j的背包中的最大价值
    int[][] path = new int[n+1][m+1];//表示商品放入的情况

    //初始化第一行和第一列的值为0(非必要的步骤，因为默认为0，只是为了表示当背景容量为0时，背包最大价值也为0的情况)
    for (int i = 0; i <= dp.length; i++) {
        dp[0][i] = 0;
    }
    for (int i = 0; i < dp.length; i++) {
        dp[i][0] = 0;
    }

    //动态规划算法解决01背包问题
    for (int i = 1; i < dp.length; i++) {//不处理第一行为0的数据
        for (int j = 1; j < dp[i].length; j++) { //不处理第一列为0的数据
            //表示当前物品的重量大于背包容量，因为i = 1,如果不-1则会直接取到第二个物品重量
            if (weight[i-1] > j){
                // 当准备加入新增的商品的容量大于当前背包的容量时，就直接使用上一个单元格的装入策略
                dp[i][j] = dp[i-1][j];
            }else { //包括了weight[i-1] < j 和 weight[i-1] = j 的情况
                //因为i和j都是从1开始的，因此必须-1，否则都会取到数组内第二个数
                // dp[i][j]=Math.max(dp[i-1][j], value[i-1]+dp[i-1][j-weight[i-1]]);
                //使用上面的Math的api无法记录物品放入的情况，因此改成使用下面的判断
                if (dp[i-1][j] < value[i-1]+dp[i-1][j-weight[i-1]]){
                    dp[i][j] = value[i-1]+dp[i-1][j-weight[i-1]];
                    path[i][j] = 1;//将当前放入情况记录到path数组中
                }else {
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
    }

    //输出商品放入的情况
    int i = path.length - 1;//行的最大下标
    int j = path[0].length - 1;//列的最大下标

    while (i > 0 && j > 0){ //从path的最后开始找
        if (path[i][j] == 1){
            System.out.printf("第%d个物品放入背包中\n",i);
            //上面输出了当前放入的包后需要减去当前放入商品的容量，因为这是个01背包，每个商品只会放一次
            j -= weight[i-1];
        }
        i--; //找下一个存放的商品
    }

    //输出二维数组
    for (int[] d : dp) {
        for (int ii : d) {
            System.out.print(ii + "\t");
        }
        System.out.println();
    }
}

KMP算法

• 什么是KMP算法

常用于在一个文本串S内查找一个模式串P的出现位置。

Knuth-Morris-Pratt 也称为字符串查找算法，简称为 “KMP算法”。

此算法由Donald Knuth、Vaughan Pratt、James H. Morris三人发表，故取这3人的姓氏命名此算法。

• 暴力匹配字符串

通过将模式串和文本串转为char型数组进行逐一匹配，失败则回溯到匹配前的下一个字符再次执行前序步骤

public static int violenceMatch(String matchStr,String str){
    char[] matchChar = matchStr.toCharArray();
    char[] strChar = str.toCharArray();
    int i = 0; //维护matchChar数组的指向
    int j = 0; //维护strChar数组的指向
    while (i < matchChar.length && j < strChar.length){
        if (matchChar[i] == strChar[j]){
            //匹配两个数组各自的下一个字符
            i++;
            j++;
        }else {
            //重置i和j的指向
            //回溯到匹配前的下一个字符继续匹配
            i = i - j + 1; //i-j表示将i调回到遍历j个数之前，+1表示为i的下个数
            j = 0;
        }
    }
    if (j == strChar.length){
        return i-j;
    }else {
        return -1;
    }
}

• KMP算法实现字符串查找的思路

KMP算法利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，

每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间

• 对KMP算法的个人理解

根据模式串的前缀得出各个下标对应的最长公共前后缀的长度，从而根据这些长度值形成前缀表

将前缀表整体右移(舍弃右边最高位)，首位补-1形成了next数组，当文本串和模式串逐一匹配时，

当出现第一个失配位(两个串的字符不同)时，假设失配位为i，根据模式串中i下标对应的最长公共

前后缀的长度x，将模式串第x位数对准文本串中的当前i的失配位处，重新进行比较，反正进行

上述步骤，直至找到一组完成匹配。

KMP字符串查找算法核心就是 模式串 => 前缀表 => next数组 => 文本串和模式串借助next数组不断匹配

/**
     * Description : kmp字符串查找算法
     * @param textStr 文本串
     * @param modelStr 模式串
**/
public static int kmpMatch(String textStr,String modelStr){
    char[] text = textStr.toCharArray();
    char[] model = modelStr.toCharArray();
    //获得辅助比较的next数组
    int[] next = getNextInt(modelStr); 
    int i = 0; //维护指向text数组的指针
    int j = 0; //维护指向model数组的指针
    while (i < text.length && j < model.length){
        if (text[i] == model[j]){ //表示当前i和j对应位字符都是一致的
            //匹配两个数组各自的下一个字符
            i++;
            j++;
        }else {
            //从next数组取出j当前失配位所对应的模式串中应该再次对比的字符下标
            j = next[j];
            //当j == -1时表示文本创和模式串中的第一个字符就不匹配
            //将指向i的指针移动至文本串的下一个字符重新与模式串第一个字符重新匹配
            if (j == -1){ 
                i += 1;
                j = 0;
            }
        }
    }
    //从上面的while循环出来之后，i已经越界，j已经越界
    //如果j == 模式串的长度代表是找到了对应字符串越界才从while来的，
    // 否则仅仅是单纯越界出来的，并没有找到对应的字符串
    if (j == model.length){
        return i-j; //i-j是返回在文本串中匹配成功字符串的头部下标
    }else { //代表没找到返回-1
        return -1;
    }
}

/**
     * Description : 根据模式串获得next数组
     * @param modelStr 模式串(字串)
**/
public static int[] getNextInt(String modelStr){
    char[] str = modelStr.toCharArray();
    int[] prefixTable = new int[modelStr.length()]; //前缀表
    int i = 1; //维护str的索引，从1开始是因为0位的字串的最长公共前后缀一定为0
    int len = 0; //维护从0到i的字串最长公共前后缀的长度
    while (i < str.length){ //遍历str数组形成前缀表
        if (str[i] == str[len]){ //表示在str数组中的i和len的数相同，
            len++; //前后缀长度+1；
            prefixTable[i] = len; //将0-i的所对应的字串的前后缀长度设置为len的值
        }else { //不匹配的情况
            len = 0; //将记录最长公共前后缀长度变量重新置为0
            prefixTable[i] = 0;//将0-i的所对应的字串的前后缀长度设置为0，表示无公共前后缀
        }
        i++; //查找从0-(i+1)位置的字串的的最长公共前后缀
    }
    //将前缀表整体右移，舍弃最高位，同时首位补-1
    int[] next = new int[str.length];
    next[0] = -1;
    for (int j = 1; j < next.length; j++) {
        next[j] = prefixTable[j-1];
    }
    return next;
}

贪心算法

• 什么是贪心算法

贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，

从而希望能够导致结果是最好或者最优的算法，它所得到的结果不一定是最优的结果(有时候会是最优解)，

但是都是相对近似(接近)最优解的结果。

贪心算法并不从整体最优上加以考虑，它所做的选择只是在某种意义上的局部最优解。

• 电台覆盖问题(贪心算法实现)

实现思路：

①将所有待覆盖地区全部加入一个集合areaList

②用一个集合selectList记录所选择的电台

③针对每个电台进行遍历，计算其能够覆盖的地区数，每一轮选择最多覆盖数的电台，

将此电台加入selectList，同时将此电台所覆盖的所有地区从areaList集合中去除。

④不断重复第③步，直至areaList集合的长度为0，此时代表已经完成对所有地区的覆盖。

public static List<String> greedy(){
    //构建存储所有电台以及电台覆盖地区信息的map集合
    HashMap<String, String[]> broadcasts = new HashMap<>();
    broadcasts.put("k1",new String[]{"北京", "上海", "天津"});
    broadcasts.put("k2",new String[]{"广州", "北京", "深圳"});
    broadcasts.put("k3",new String[]{"成都", "上海", "杭州"});
    broadcasts.put("k4",new String[]{"上海", "天津"});
    broadcasts.put("k5",new String[]{"杭州", "大连"});

    //存储所有待覆盖地区信息的set集合(自带去重复效果)
    HashSet<String> areaList = new HashSet<>();
    //返回所有(包含了所有待覆盖地区名)构成的Collection集合
    Collection<String[]> areaNames = broadcasts.values();
    for(String[] name : areaNames){
        //将所有待覆盖地区名加入到areaList集合中
        Collections.addAll(areaList, name);
    }
    //维护已选择的电台信息的集合
    List<String> selectList = new ArrayList<>();
    String maxBCIndex = "";//维护选择的最大覆盖地区的广播的名称
    while (areaList.size() != 0){
        int max = 0;
        //包含所有电台名称构成的set集合
        Set<String> broadcastName = broadcasts.keySet();
        for (String bcName : broadcastName) {
            int needCoverNum = 0; //记录当前电台所覆盖地区的个数
            String[] coverAreaArray = broadcasts.get(bcName);//当前名称对应电台覆盖地区数组
            //判断当前电台覆盖的地区在需要覆盖地区集合中的个数
            for(String area : coverAreaArray){ 
                if (areaList.contains(area)){ //逐一判断当前电台的覆盖地区是否在待覆盖地区的集合中
                    needCoverNum++;
                }
            }
            if (needCoverNum != 0){
                //下面这个比较就体现出了贪心算法的特点，每次选择的都是局部最优解
                if (max < needCoverNum){ //从所有电台中判断覆盖的地区最多的电台
                    max = needCoverNum;
                    maxBCIndex = bcName;
                }
            }
        }
        selectList.add(maxBCIndex); //将覆盖最多地区的电台加入选择电台的list集合
        String[] broadcast = broadcasts.get(maxBCIndex); //获得对应电台覆盖地区的数组
        for (String areaName : broadcast){ //逐个从待覆盖地区的集合中删除对应已覆盖的地区名
            areaList.remove(areaName);
        }
        broadcasts.remove(maxBCIndex);//从所有电台中删除已加入选择电台集合中的电台名
    }
    return selectList;
}

• 贪心算法和动态规划算法的区别

①动态规划类似于穷举法，记录了之前的结果，不需要进行重复的计算，可以利用前边的结果（状态方程），

一般复杂度比贪心高，但是可以得到全局最优解。

②贪心算法每次只考虑当前，不保证能得到全局最优，只保证当前最优，都是先选择再证明，一般复杂度比较低。

③贪心算法的基本要素：最优子结构性质和贪心选择性质

​ 动态规划的基本要素：最优子结构性质和重叠子问题性质

④动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常自顶向下的方式进行。

自底向上：换句话理解说就是从小到大，通过不断解决小问题从而解决原问题

自顶向下：换句话理解就是从原问题入手，通过不断分解成小问题，从而解决原问题

⑤贪心算法每次都将问题分解成一个子问题，再将所有子问题的解进行融合，从而解决原问题。

动态规划将计算过程中的结果保存下来重复使用，避免无必要的重复计算。

---

未完待续~剩下内容，有机会再补充。